Tutorial 10: Fourier Series
Tutorial Question
-
Find the fundamental period of the following function:
a.
b.
c.
d.
Solutiona.
b.
c.
d.
-
Sketch the given function and find the Fourier Series.
a.
b.
c.
Solutiona.
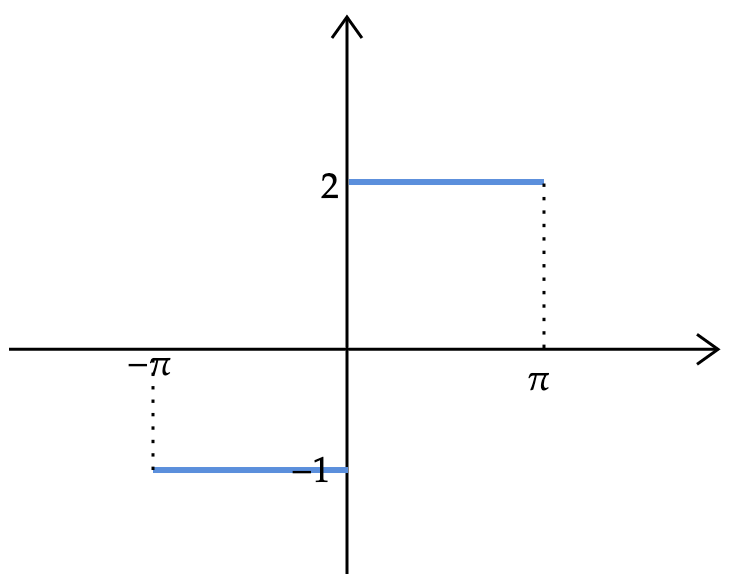
b.
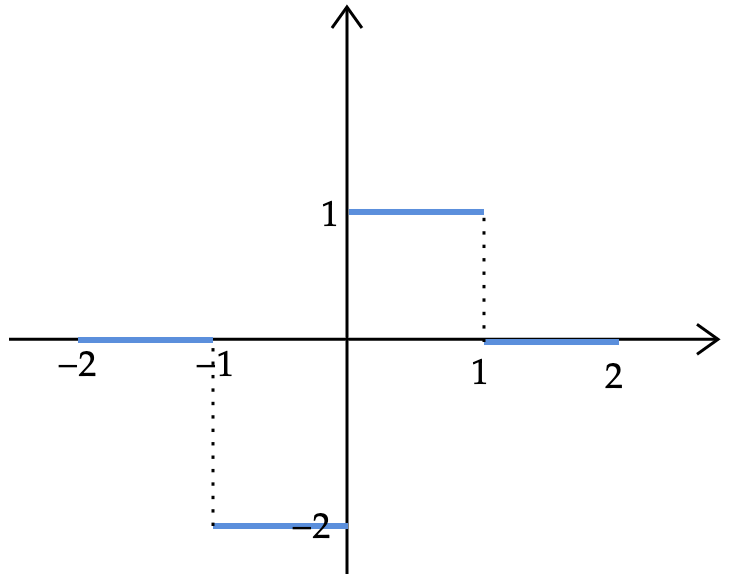
c.
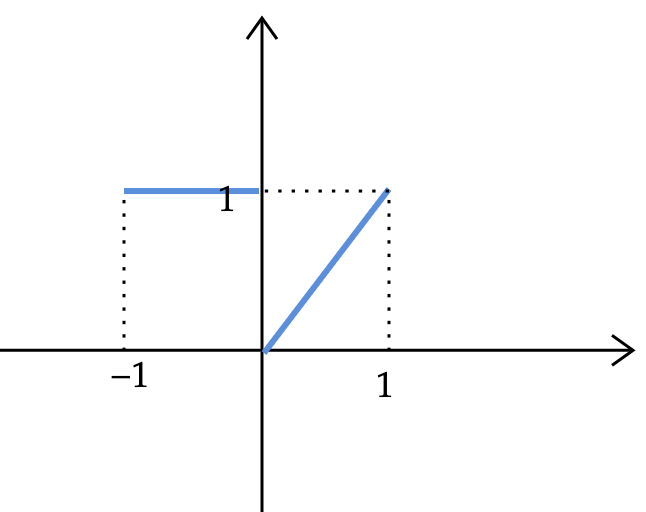
-
Even and Odd Functions. Sketch the given functions, . Determine whether it is an even, odd or neither odd nor even. For part (a) and (b), find the appropriate Fourier Cosine or Fourier Sine Series.
a.
b.
c.
(Do not find the Fourier Series for 3c)
d.
(Do not find the Fourier Series for 3d)
Solutiona.
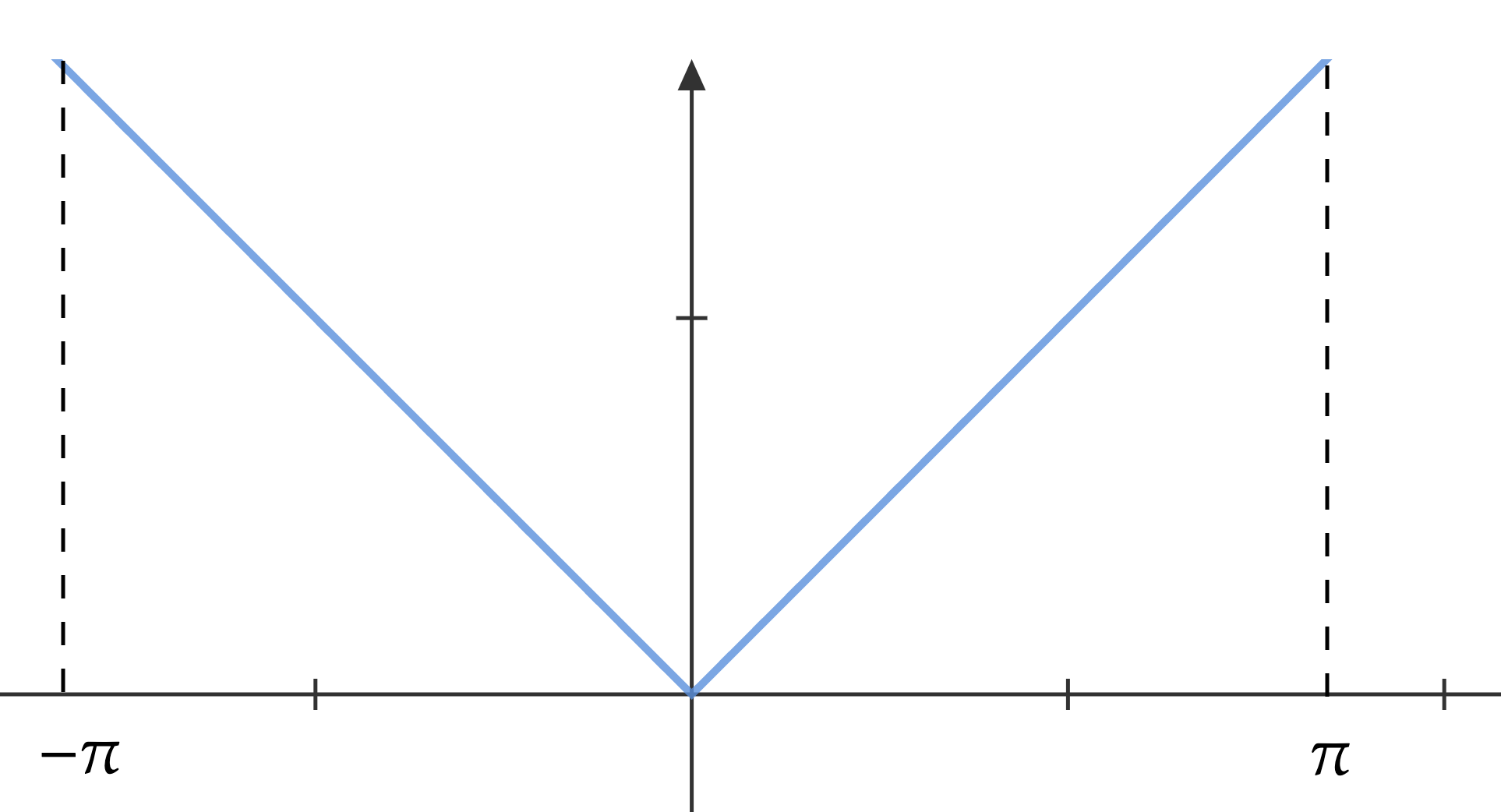
Since is an even function, we expand in a cosine series:
Thus,
b.
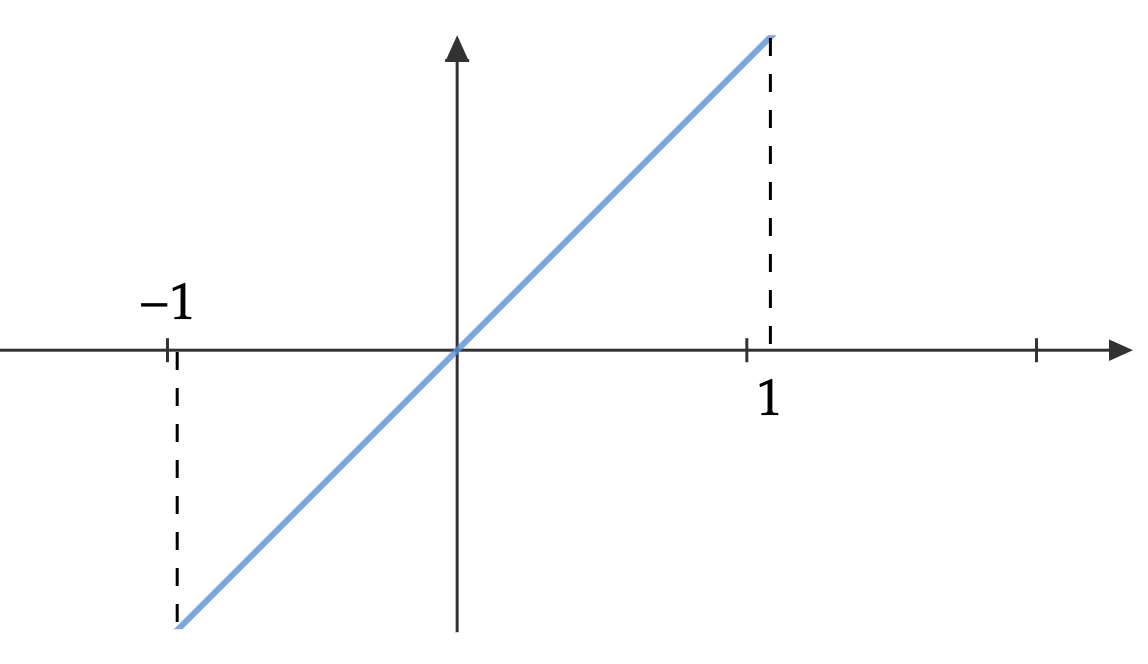
It is an odd function →
c.
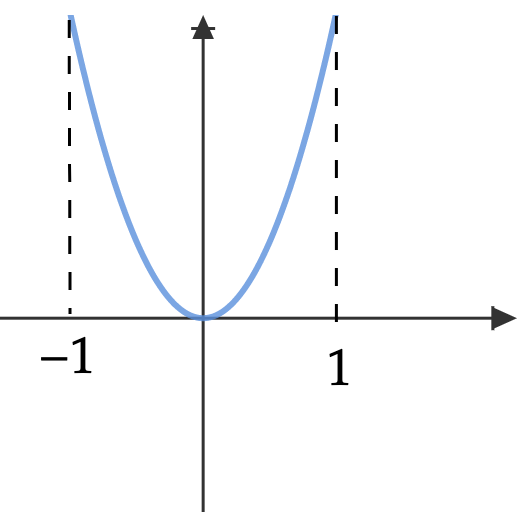
Even function
d.
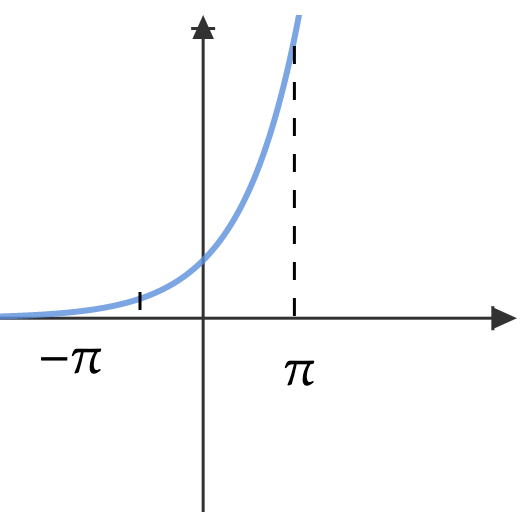
Neither odd or even
-
Solve the following questions:
a. Obtain the Fourier series for a periodic function with period :
b. Obtain the Fourier series for a periodic function with period :
c. Differentiate the Fourier series in (a) to obtain
d. Find the Fourier series of by using result in part (c) and compare it with (b).
Solutiona. Since is an even function,
b. since . Thus, it is an odd function.
c.
d.
The answer obtained by differentiation is faster and the answer is the same as 4(b).
-
Consider the following ODE which represents an undamped mass-spring system:
where is a periodic function as shown in Fig. 1. Obtain a particular solution for the ODE.
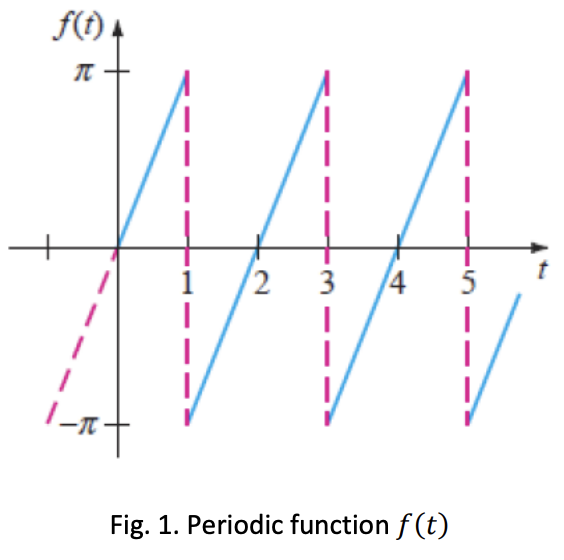 Solution
SolutionWe expand as an odd function.
We assume a particular solution of the form