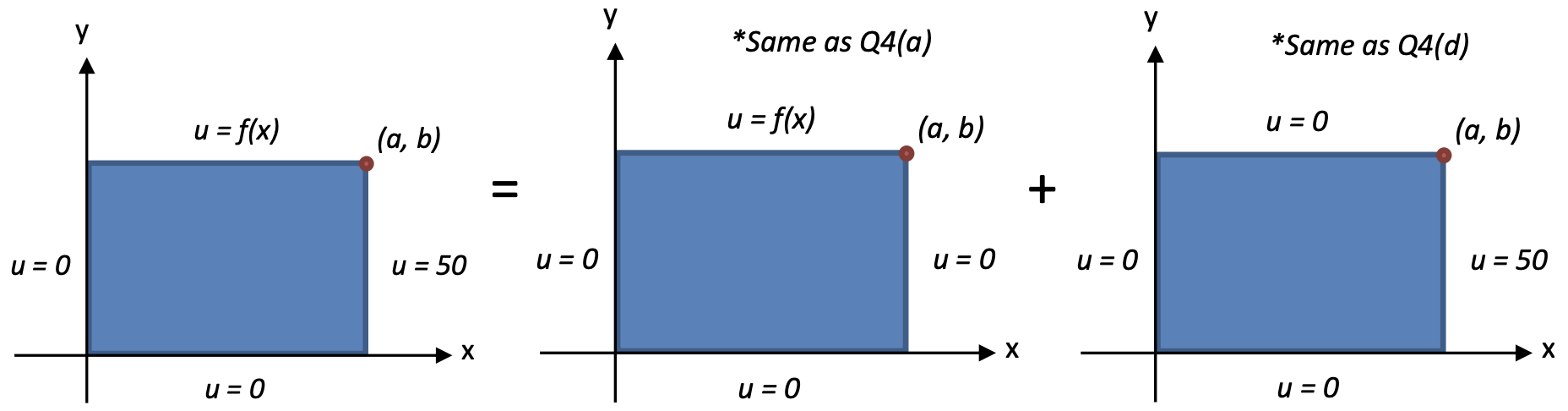
To solve the Laplace equation easily, we use the boundary condition 1 & 2 with zeros first.
For Case 1: λ=0
BC 1: u1(0,y)=(c1+c2y)(c3+c4(0))=0
→ Assume c1+c2y=0;c3=0
→u1(x,y)=(c1+c2y)(c4x)
BC 2: u1(a,y)=(c1+c2y)(c4a)=0
→(c1+c2y)=0 & a=0; hence c4=0
→u1(x,y)=(c1+c2y)(0)=0
∴u1=0; No solution for case 1
For Case 2: λ=−α2,α>0
BC 1: u2(0,y)=(c5cos(αy)+c6sin(αy))(c7cosh(0)+c8sinh(0))=0
(c5cos(αy)+c6sin(αy))(c7)=0
→(c5cos(αy)+c6sin(αy))=0; hence c7=0
→u2(x,y)=(c5cos(αy)+c6sin(αy))(c8sinh(αx))
BC 2: u2(a,y)=(c5cos(αy)+c6sin(αy))(c8sinh(αa))=0
→(c5cos(αy)+c6sin(αy))=0,sinh(αa)=0; hence c8=0
→u2(x,y)=(c5cos(αy)+c6sin(αy))(0)=0
∴u2=0; No solution for case 2
For Case 3: λ=+α2,α>0
BC 1: u3(0,y)=(c9cosh(αy)+c10sinh(αy))(c11cos(0)+c12sin(0))=0
(c9cosh(αy)+c10sinh(αy))(c11)=0
→(c9cosh(αy)+c10sinh(αy))=0; hence c11=0
→u3(x,y)=(c9cosh(αy)+c10sinh(αy))(c12sin(αx))
BC 2: u3(a,y)=(c9cosh(αy)+c10sinh(αy))(c12sin(αa))=0
→(c9cosh(αy)+c10sinh(αy)),c12=0; hence sin(αa)=0 when αb=nπ,α=bnπ where n=1,2,3,…
∴u3,n=(c9,ncosh(anπy)+c10,nsinh(anπy))(c12,nsin(αx))=(A3,ncosh(anπy)+B3,nsinh(anπy))(sin(anπx)) where n=1,2,3,…
Eigenvalue, λn=+αn2=(anπ)2
Eigenfunction, u3,n=(A3,ncosh(anπy)+B3,nsinh(anπy))(sin(anπx))
∴utotal (x,y)=∑n=1∞(A3,ncosh(anπy)+B3,nsinh(anπy))(sin(anπx))
BC 3:
utotal (x,0)=n=1∑∞(A3,ncosh(anπ(0))+B3,nsinh(anπ(0)))(sin(anπx))=0=n=1∑∞(A3,n)(sin(anπx))=0
Recall Half-Range Fourier Sine Series Expansion:
A3,n=L2∫0τf(x)sin(anπx)dx=0
utotal (x,y)=∑n=1∞(B3,nsinh(anπy))(sin(anπx))
BC 4: utotal (x,b)=∑n=1∞(B3,nsinh(anπb))(sin(anπx))=f(x)
Half-Range Fourier Sine Series Expansion:
f(x)=∑n=1∞(B3,nsinh(anπb))(sin(anπx))
where B3,nsinh(anπb)=L2∫0τf(x)sinnωxdx,ω=aπ,p=ω2π=2a,L=2p=a,τ=a
B3,nsinh(anπb)=a2∫0af(x)sinnaπxdx
B3,n=asinh(anπb)2∫0af(x)sinnaπxdx
∴utotal (x,y)=∑n=1∞(asinh(anπb)2∫0af(x)sinnaπxdxsinh(anπy))(sin(anπx))