Skip to main content

Tutorial 8: Laplace Transform

Tutorial Question
    1. Using the definition of Laplace transform, find the transform L{f(t)}\mathcal{L}\{f(t)\}. Show the details of your integration.

    i. f(t)=7t−5f(t)=7t-5

    ii. f(t)=sinh⁡ktf(t)=\sinh kt

    iii. f(t)=e−tcosh⁡tf(t)=e^{-t}\cosh t

    iv. f(t)=tsin⁡tf(t)=t\sin t

    v.

    vi.

    vii.

    viii.

    Solution

    i.

    L(7t−5)=∫0∞(7t−5)e−stdt=∫0∞7te−stdt−∫0∞5e−stdt=−7ste−st∣0∞−(−7s)∫0∞e−stdt+5se−st∣0∞=−7s2e−st∣0∞−5s=7s2−5s\begin{aligned}\mathcal{L}(7 t-5) &=\int_{0}^{\infty}(7 t-5) e^{-s t} d t \\&=\int_{0}^{\infty} 7 t e^{-s t} d t-\int_{0}^{\infty} 5 e^{-s t} d t \\&=-\left.\frac{7}{s} t e^{-s t}\right|_{0} ^{\infty}-\left(-\frac{7}{s}\right) \int_{0}^{\infty} e^{-s t} d t+\left.\frac{5}{s} e^{-s t}\right|_{0} ^{\infty} \\&=-\left.\frac{7}{s^{2}} e^{-s t}\right|_{0} ^{\infty}-\frac{5}{s} \\&=\frac{7}{s^{2}}-\frac{5}{s}\end{aligned}

    ii.

    L(sinh⁡kt)=∫0∞(sinh⁡kt)e−stdt=∫0∞(ekt−e−kt2)e−stdt=12(∫0∞ekte−stdt−∫0∞e−kte−stdt)=12(∫0∞e(k−s)tdt−∫0∞e−(k+s)tdt)=12(1k−se(k−s)t∣0∞+1k+se−(k+s)t∣0∞)=12(−1k−s−1k+s)=12(1s−k−1s+k)=12(s+k−s+k(s−k)(s+k))=ks2−k2\begin{aligned}\mathcal{L}(\sinh k t)&=\int_{0}^{\infty}(\sinh k t) e^{-s t} d t\\&=\int_{0}^{\infty}\left(\frac{e^{k t}-e^{-k t}}{2}\right) e^{-s t} d t \\&=\frac{1}{2}\left(\int_{0}^{\infty} e^{k t} e^{-s t} d t-\int_{0}^{\infty} e^{-k t} e^{-s t} d t\right) \\&=\frac{1}{2}\left(\int_{0}^{\infty} e^{(k-s) t} d t-\int_{0}^{\infty} e^{-(k+s) t} d t\right) \\&=\frac{1}{2}\left(\left.\frac{1}{k-s} e^{(k-s) t}\right|_{0} ^{\infty}+\left.\frac{1}{k+s} e^{-(k+s) t}\right|_{0} ^{\infty}\right) \\&=\frac{1}{2}\left(-\frac{1}{k-s}-\frac{1}{k+s}\right) \\&=\frac{1}{2}\left(\frac{1}{s-k}-\frac{1}{s+k}\right) \\&=\frac{1}{2}\left(\frac{s+k-s+k}{(s-k)(s+k)}\right) \\&=\frac{k}{s^{2}-k^{2}}\end{aligned}

    iii.

    L(e−tcosh⁡t)=∫0∞e−t(et+e−t2)e−stdt=12(∫0∞e−tete−stdt+∫0∞e−te−te−stdt)=12(∫0∞e−stdt+∫0∞e−(2+s)tdt)=12(−1se−st∣0∞−1s+2e(s+2)t∣0∞)=12(1s+1s+2)\begin{aligned}\mathcal{L}\left(e^{-t} \cosh t\right)&=\int_{0}^{\infty} e^{-t}\left(\frac{e^{t}+e^{-t}}{2}\right) e^{-s t} d t\\&=\frac{1}{2}\left(\int_{0}^{\infty} e^{-t} e^{t} e^{-s t} d t+\int_{0}^{\infty} e^{-t} e^{-t} e^{-s t} d t\right) \\&=\frac{1}{2}\left(\int_{0}^{\infty} e^{-s t} d t+\int_{0}^{\infty} e^{-(2+s) t} d t\right) \\&=\frac{1}{2}\left(-\left.\frac{1}{s} e^{-s t}\right|_{0} ^{\infty}-\left.\frac{1}{s+2} e^{(s+2) t}\right|_{0} ^{\infty}\right) \\&=\frac{1}{2}\left(\frac{1}{s}+\frac{1}{s+2}\right)\end{aligned}

    iv.

    L(tsin⁡t)=∫0∞(tsin⁡t)e−stdt\mathcal{L}(t \sin t)=\int_{0}^{\infty}(t \sin t) e^{-s t} d t

    Let u=t,dv=e−stsin⁡tu=t, d v=e^{-s t} \sin t

    v=∫e−stsin⁡tdt=−1se−stsin⁡t+1s∫e−stcos⁡tdt=−1se−stsin⁡t+1s(−1se−stcos⁡t−1s∫e−stsin⁡tdt)=−1se−stsin⁡t−1s2e−stcos⁡t−1s2∫e−stsin⁡tdt(1+1s2)∫e−stsin⁡tdt=−1se−stsin⁡t−1s2e−stcos⁡tv=∫e−stsin⁡tdt=−ss2+1e−stsin⁡t−1s2+1e−stcos⁡t\begin{aligned}v=\int e^{-s t} \sin t d t&=-\frac{1}{s} e^{-s t} \sin t+\frac{1}{s} \int e^{-s t} \cos t d t \\&=-\frac{1}{s} e^{-s t} \sin t+\frac{1}{s}\left(-\frac{1}{s} e^{-s t} \cos t-\frac{1}{s} \int e^{-s t} \sin t d t\right)\\& =-\frac{1}{s} e^{-s t} \sin t-\frac{1}{s^{2}} e^{-s t} \cos t-\frac{1}{s^{2}} \int e^{-s t} \sin t d t \\ \left(1+\frac{1}{s^{2}}\right) \int e^{-s t} \sin t d t&=-\frac{1}{s} e^{-s t} \sin t-\frac{1}{s^{2}} e^{-s t} \cos t \\ v=\int e^{-s t} \sin t d t&=-\frac{s}{s^{2}+1} e^{-s t} \sin t-\frac{1}{s^{2}+1} e^{-s t} \cos t \\\end{aligned}L(tsin⁡t)=t(−ss2+1e−stsin⁡t−1s2+1e−stcos⁡t)∣0∞−∫0∞(−ss2+1e−stsin⁡t−frac1s2+1e−stcos⁡t)dt=−sts2+1e−stsin⁡t∣0∞−ts2+1e−stcos⁡t∣0∞+ss2+1∫0∞e−stsin⁡tdt+1s2+1∫0∞e−stcos⁡tdt\begin{aligned}\mathcal{L}(t \sin t)&=\left.t\left(-\frac{s}{s^{2}+1} e^{-s t} \sin t-\frac{1}{s^{2}+1} e^{-s t} \cos t\right)\right|_{0} ^{\infty}\\ \qquad &-\int_{0}^{\infty}\left(-\frac{s}{s^{2}+1} e^{-s t} \sin t-\\frac{1}{s^{2}+1} e^{-s t} \cos t\right) d t \\& =-\left.\frac{s t}{s^{2}+1} e^{-s t} \sin t\right|_{0} ^{\infty}-\left.\frac{t}{s^{2}+1} e^{-s t} \cos t\right|_{0} ^{\infty}\\&\quad+\frac{s}{s^{2}+1} \int_{0}^{\infty} e^{-s t} \sin t d t+ \frac{1}{s^{2}+1} \int_{0}^{\infty} e^{-s t} \cos t d t \\\end{aligned}∫0∞e−stsin⁡tdt=−ss2+1e−stsin⁡t∣0∞−1s2+1e−stcos⁡t∣0∞=1s2+1\begin{aligned} \int_{0}^{\infty} e^{-s t} \sin t d t&=-\left.\frac{s}{s^{2}+1} e^{-s t} \sin t\right|_{0} ^{\infty}-\left.\frac{1}{s^{2}+1} e^{-s t} \cos t\right|_{0} ^{\infty} \\& =\frac{1}{s^{2}+1} \end{aligned}∫0∞e−stcos⁡tdt=−1se−stcos⁡t∣0∞−1s∫0∞e−stsin⁡tdt=1s−1s(1s2+1)=ss2+1\begin{aligned} \int_{0}^{\infty} e^{-s t} \cos t d t&=-\left.\frac{1}{s} e^{-s t} \cos t\right|_{0} ^{\infty}-\frac{1}{s} \int_{0}^{\infty} e^{-s t} \sin t d t \\& =\frac{1}{s}-\frac{1}{s}\left(\frac{1}{s^{2}+1}\right)=\frac{s}{s^{2}+1} \end{aligned}L(tsin⁡t)=ss2+1(1s2+1)+1s2+1(ss2+1)=2s(s2+1)2\begin{aligned}\mathcal{L}(t \sin t)&=\frac{s}{s^{2}+1}\left(\frac{1}{s^{2}+1}\right)+\frac{1}{s^{2}+1}\left(\frac{s}{s^{2}+1}\right) \\ & =\frac{2 s}{\left(s^{2}+1\right)^{2}} \end{aligned}

    v.

    f(t)={−10<t<12t>1f(t)=\left\{\begin{array}{cc}-1 & 0<t<1 \\ 2 & t>1\end{array}\right.L{f(t)}=∫01−e−stdt+2∫1∞e−stdt=1se−st∣01−2se−st∣1∞=1se−s−1s−(0−2se−s)=3se−s−1s=1s(3e−s−1)\begin{aligned}\mathcal{L}\{f(t)\} &=\int_{0}^{1}-e^{-s t} d t+2 \int_{1}^{\infty} e^{-s t} d t \\&=\left.\frac{1}{s} e^{-s t}\right|_{0} ^{1}-\left.\frac{2}{s} e^{-s t}\right|_{1} ^{\infty}\\& =\frac{1}{s} e^{-s}-\frac{1}{s}-\left(0-\frac{2}{s} e^{-s}\right)\\&=\frac{3}{s} e^{-s}-\frac{1}{s} \\ &=\frac{1}{s}\left(3 e^{-s}-1\right)\end{aligned}

    vi.

    f(t)={00<t<12t−2t>1f(t)=\left\{\begin{array}{cc}0 & 0<t<1 \\2 t-2 & t>1\end{array}\right. L{f(t)}=∫1∞(2t−2)e−stdt=−2ste−st∣1∞+2s∫1∞e−stdt+2se−st∣1∞=2se−s+2s[−1se−st]1∞−2se−s=2s2e−s\begin{aligned}\mathcal{L}\{f(t)\}&=\int_{1}^{\infty}(2 t-2) e^{-s t} d t \\& =-\left.\frac{2}{s} t e^{-s t}\right|_{1} ^{\infty}+\frac{2}{s} \int_{1}^{\infty} e^{-s t} d t+\left.\frac{2}{s} e^{-s t}\right|_{1} ^{\infty} \\& =\frac{2}{s} e^{-s}+\frac{2}{s}\left[-\frac{1}{s} e^{-s t}\right]_{1}^{\infty}-\frac{2}{s} e^{-s} \\& =\frac{2}{s^{2}} e^{-s} \end{aligned}

    vii.

    f(t)={t0<t<12−t1<t<20t>2 f(t)=\left\{\begin{array}{cc}t & 0<t<1 \\2-t & 1<t<2 \\0 & t>2\end{array}\right. L{f(t)}=∫01te−stdt+∫12(2−t)e−stdt=−1ste−st∣01+1s∫01e−stdt−1s(2−t)e−st∣12−1s∫12e−stdt=−1se−s+1s[−1se−st]01+1se−s−1s[−1se−st]12=1s2(−e−s+1)−1s2(−e−2s+e−s)=1s2(1−2e−s+e−2s)\begin{aligned}\mathcal{L}\{f(t)\}&=\int_{0}^{1} t e^{-s t} d t+\int_{1}^{2}(2-t) e^{-s t} d t\\&=-\left.\frac{1}{s} t e^{-s t}\right|_{0} ^{1}+\frac{1}{s} \int_{0}^{1} e^{-s t} d t-\left.\frac{1}{s}(2-t) e^{-s t}\right|_{1} ^{2}-\frac{1}{s} \int_{1}^{2} e^{-s t} d t \\ &=-\frac{1}{s} e^{-s}+\frac{1}{s}\left[-\frac{1}{s} e^{-s t}\right]_{0}^{1}+\frac{1}{s} e^{-s}-\frac{1}{s}\left[-\frac{1}{s} e^{-s t}\right]_{1}^{2} \\ &=\frac{1}{s^{2}}\left(-e^{-s}+1\right)-\frac{1}{s^{2}}\left(-e^{-2 s}+e^{-s}\right) \\ &=\frac{1}{s^{2}}\left(1-2 e^{-s}+e^{-2 s}\right)\end{aligned}

    viii.

    f(t)={1−t0<t<10t>1f(t)=\left\{\begin{array}{cc}1-t & 0<t<1 \\ 0 & t>1\end{array}\right.L{f(t)}=∫01(1−t)e−stdt=−1s(1−t)e−st∣01−1s∫01e−stdt=1s−1s[−1se−st]01=1s+1s2e−s−1s2\begin{aligned}\mathcal{L}\{f(t)\}&=\int_{0}^{1}(1-t) e^{-s t} d t\\&=-\left.\frac{1}{s}(1-t) e^{-s t}\right|_{0} ^{1}-\frac{1}{s} \int_{0}^{1} e^{-s t} d t\\& =\frac{1}{s}-\frac{1}{s}\left[-\frac{1}{s} e^{-s t}\right]_{0}^{1} \\& =\frac{1}{s}+\frac{1}{s^{2}} e^{-s}-\frac{1}{s^{2}}\end{aligned}

  2. Referring to the Laplace transform table, find the transform L{f(t)}\mathcal{L}\{f(t)\}. Show the modification details that you need to do before the transform can be done.

    i. f(t)=(t+1)3f(t)=(t+1)^3

    ii. f(t)=sin⁡2tcos⁡2tf(t)=\sin2t\cos2t

    iii. f(t)=ke−atcos⁡ωtf(t)=ke^{-at}\cos\omega t

    iv. f(t)=sin⁡(4t+5)f(t)=\sin(4t+5)

    v. f(t)=t3e−2tf(t)=t^3e^{-2t}

    vi. f(t)=(1−et+3e−4t)cos⁡5tf(t)=(1-e^t+3e^{-4t})\cos5t

    vii. f(t)=(3t+1)u(t−1)f(t)=(3t+1)u(t-1)

    viii. f(t)=sin⁡tu(t−π2)f(t)=\sin tu\left(t-\frac{\pi}{2}\right)

    Solution

    i.

    L{(t+1)3}=L(t3+3t2+3t+1)=3!s4+3(2!s3)+3(1s2)+1s=6s4+6s3+3s2+1s\begin{aligned}\mathcal{L}\left\{(t+1)^{3}\right\}&= \mathcal{L}\left(t^{3}+3 t^{2}+3 t+1\right) \\&=\frac{3 !}{s^{4}}+3\left(\frac{2 !}{s^{3}}\right)+3\left(\frac{1}{s^{2}}\right)+\frac{1}{s} \\&=\frac{6}{s^{4}}+\frac{6}{s^{3}}+\frac{3}{s^{2}}+\frac{1}{s}\end{aligned}

    ii.

    L(sin⁡2tcos⁡2t)=L(12sin⁡4t)=2s2+16\begin{aligned}\mathcal{L}(\sin 2 t \cos 2 t)&=\mathcal{L}\left(\frac{1}{2} \sin 4 t\right)\\&=\frac{2}{s^{2}+16}\end{aligned}

    iii.

    L(ke−atcos⁡ωt)=k(s+a)(s+a)2+ω2\mathcal{L}\left(k e^{-a t} \cos \omega t\right)=\frac{k(s+a)}{(s+a)^{2}+\omega^{2}}

    iv.

    L{sin⁡(4t+5)}=L(sin⁡4tcos⁡5+sin⁡5cos⁡4t)=cos⁡5(4s2+16)+sin⁡5(ss2+16)=4cos⁡5+(cos⁡5)ss2+16\begin{aligned}\mathcal{L}\{\sin (4 t+5)\}&=\mathcal{L}(\sin 4 t \cos 5+\sin 5 \cos 4 t)\\&=\cos 5\left(\frac{4}{s^{2}+16}\right)+\sin 5\left(\frac{s}{s^{2}+16}\right) \\&=\frac{4 \cos 5+(\cos 5) s}{s^{2}+16}\end{aligned}

    v.

    L(t3e−2t)=3!(s+2)4\mathcal{L}\left(t^{3} e^{-2 t}\right)=\frac{3 !}{(s+2)^{4}}

    vi.

    L{(1−et+3e−4t)cos⁡5t}=L(cos⁡5t−etcos⁡5t+3e−4tcos⁡5t)=ss2+25−s−1(s−1)2+25+3(s+4)(s+4)2+25\begin{aligned}\mathcal{L}\left\{\left(1-e^{t}+3 e^{-4 t}\right) \cos 5 t\right\}&= \mathcal{L}\left(\cos 5 t-e^{t} \cos 5 t+3 e^{-4 t} \cos 5 t\right) \\&=\frac{s}{s^{2}+25}-\frac{s-1}{(s-1)^{2}+25}+\frac{3(s+4)}{(s+4)^{2}+25}\end{aligned}

    vii.

    L{(3t+1)u(t−1)}=3L{(t−1)u(t−1)}+4u(t−1)=3e−ss2+4e−ss\begin{aligned}\mathcal{L}\{(3 t+1) u(t-1)\}&=3 \mathcal{L}\{(t-1) u(t-1)\}+4 u(t-1)\\&=\frac{3 e^{-s}}{s^{2}}+\frac{4 e^{-s}}{s}\end{aligned}

    viii.

    L{sin⁡tu(t−π2)}=L{cos⁡(t−π2)u(t−π2)}=se−πs/2s2+1\begin{aligned}\mathcal{L}\left\{\sin t u\left(t-\frac{\pi}{2}\right)\right\}&=\mathcal{L}\left\{\cos \left(t-\frac{\pi}{2}\right) u\left(t-\frac{\pi}{2}\right)\right\}\\&=\frac{s e^{-\pi s / 2}}{s^{2}+1}\end{aligned}

  3. Given L{f(t)}\mathcal{L}\{f(t)\}, find f(t)f(t). Show the details of your work, including the partial fraction expansion if necessary.

    i. L−1(1s2−48s5)\mathcal{L}^{-1}\left(\frac{1}{s^2}-\frac{48}{s^5}\right)

    ii. L−1{(s+1)3s4}\mathcal{L}^{-1}\left\{\frac{(s+1)^3}{s^4}\right\}

    iii. L−1(4s4s2+1)\mathcal{L}^{-1}\left(\frac{4s}{4s^2+1}\right)

    iv. L−1(2s−6s2+9)\mathcal{L}^{-1}\left(\frac{2s-6}{s^2+9}\right)

    v. L−1{0.9s(s−0.1)(s+0.2)}\mathcal{L}^{-1}\left\{\frac{0.9s}{(s-0.1)(s+0.2)}\right\}

    vi. L−1{s−3(s−3)(s+3)}\mathcal{L}^{-1}\left\{\frac{s-3}{(s-\sqrt{3})(s+\sqrt{3})}\right\}

    vii. L−1{s(s+2)(s2+4)}\mathcal{L}^{-1}\left\{\frac{s}{(s+2)(s^2+4)}\right\}

    viii. L−1{ss2+4s+5}\mathcal{L}^{-1} \left\{\frac{s}{s^2+4s+5}\right\}

    ix. L−1{se−πs2s2+4}\mathcal{L}^{-1}\left\{\frac{se^{-\frac{\pi s}{2}}}{s^2+4}\right\}

    x. L−1{e−2ss2(s−1)}\mathcal{L}^{-1} \left\{\frac{e^{-2s}}{s^2(s-1)}\right\}

    Solution

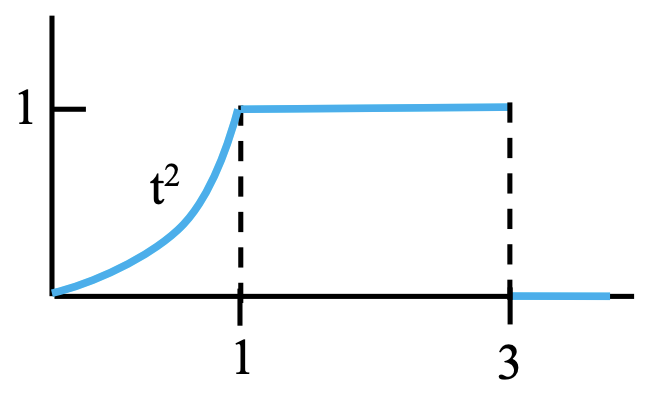
    i.

    L−1(1s2−48s5)=L−1(1s2−484!4!s5)=t−2t4\begin{aligned}\mathcal{L}^{-1}\left(\frac{1}{s^{2}}-\frac{48}{s^{5}}\right)&=\mathcal{L}^{-1}\left(\frac{1}{s^{2}}-\frac{48}{4 !} \frac{4 !}{s^{5}}\right)\\&=t-2 t^{4}\end{aligned}

    ii.

    L−1{(s+1)3s4}=L−1(s3+3s2+3s+1s4)=L−1(1s+3s2+322s3+163!s4)=1+3t+32t2+16t3\begin{aligned}\mathcal{L}^{-1}\left\{\frac{(s+1)^{3}}{s^{4}}\right\}&=\mathcal{L}^{-1}\left(\frac{s^{3}+3 s^{2}+3 s+1}{s^{4}}\right)\\&=\mathcal{L}^{-1}\left(\frac{1}{s}+\frac{3}{s^{2}}+\frac{3}{2} \frac{2}{s^{3}}+\frac{1}{6} \frac{3 !}{s^{4}}\right) \\ &=1+3 t+\frac{3}{2} t^{2}+\frac{1}{6} t^{3}\end{aligned}

    iii.

    L−1(4s4s2+1)=L−1(ss2+14)=cos⁡12t\begin{aligned} \mathcal{L}^{-1}\left(\frac{4 s}{4 s^{2}+1}\right) &=\mathcal{L}^{-1}\left(\frac{s}{s^{2}+\frac{1}{4}}\right) \\ &=\cos \frac{1}{2} t \end{aligned}

    iv.

    L−1(2s−6s2+9)=L−1(2ss2+9−23s2+9)=2cos⁡3t−2sin⁡3t\begin{aligned} \mathcal{L}^{-1}\left(\frac{2 s-6}{s^{2}+9}\right)&=\mathcal{L}^{-1}\left(2 \frac{s}{s^{2}+9}-2 \frac{3}{s^{2}+9}\right)\\ &=2 \cos 3 t-2 \sin 3 t \end{aligned}

    v.

    Let 0.9s(s−0.1)(s+0.2)=As−0.1+Bs+0.2\frac{0.9 s}{(s-0.1)(s+0.2)}=\frac{A}{s-0.1}+\frac{B}{s+0.2} ⇒ A=0.3,B=0.6A=0.3,\quad B=0.6

    L−1{0.9s(s−0.1)(s+0.2)}=L−1{0.31s−0.1+0.61s+0.2}=0.3e0.1t+0.6e−0.2t\begin{aligned} \mathcal{L}^{-1}\left\{\frac{0.9 s}{(s-0.1)(s+0.2)}\right\} &=\mathcal{L}^{-1}\left\{0.3 \frac{1}{s-0.1}+0.6 \frac{1}{s+0.2}\right\} \\ &=0.3 e^{0.1 t}+0.6 e^{-0.2 t} \end{aligned}

    vi.

    L−1{s−3(s−3)(s+3)}=L−1(ss2−3−3s2−3)=cosh⁡3t−3sinh⁡3t\begin{aligned}\mathcal{L}^{-1}\left\{\frac{s-3}{(s-\sqrt{3})(s+\sqrt{3})}\right\}&=\mathcal{L}^{-1}\left(\frac{s}{s^{2}-3}-\frac{3}{s^{2}-3}\right)\\&=\cosh \sqrt{3} t-\sqrt{3} \sinh \sqrt{3} t\end{aligned}

    vii.

    Let s(s+2)(s2+4)=As+2+Bs+Cs2+4\frac{s}{(s+2)\left(s^{2}+4\right)}=\frac{A}{s+2}+\frac{B s+C}{s^{2}+4} ⇒ A=−14,B=14,C=12A=-\frac{1}{4}, \quad B=\frac{1}{4}, \quad C=\frac{1}{2}

    L−1{s(s+2)(s2+4)}=L−1(14ss2+4+142s2+4−141s+2)=14cos⁡2t+14sin⁡2t−14e−2t\begin{aligned} \mathcal{L}^{-1}\left\{\frac{s}{(s+2)\left(s^{2}+4\right)}\right\} &=\mathcal{L}^{-1}\left(\frac{1}{4} \frac{s}{s^{2}+4}+\frac{1}{4} \frac{2}{s^{2}+4}-\frac{1}{4} \frac{1}{s+2}\right) \\ &=\frac{1}{4} \cos 2 t+\frac{1}{4} \sin 2 t-\frac{1}{4} e^{-2 t} \end{aligned}

    viii.

    L−1{ss2+4s+5}=L−1{(s+2)−2(s+2)2+1}=e−2tcos⁡t−2e−2tsin⁡t\begin{aligned}\mathcal{L}^{-1}\left\{\frac{s}{s^{2}+4 s+5}\right\}&=\mathcal{L}^{-1}\left\{\frac{(s+2)-2}{(s+2)^{2}+1}\right\}\\&=e^{-2 t} \cos t-2 e^{-2 t} \sin t\end{aligned}

    ix.

    L−1{se−πs/2s2+4}=cos⁡2(t−π2)u(t−π2)\mathcal{L}^{-1}\left\{\frac{s e^{-\pi s / 2}}{s^{2}+4}\right\}=\cos 2\left(t-\frac{\pi}{2}\right) u\left(t-\frac{\pi}{2}\right)

    x.

    Let 1s2(s−1)=As+Bs2+Cs−1\frac{1}{s^{2}(s-1)}=\frac{A}{s}+\frac{B}{s^{2}}+\frac{C}{s-1} ⇒ A=−1,B=−1,C=1A=-1, \quad B =-1, \quad C=1

    L−1{e−2ss2(s−1)}=L−1(−e−2ss−e−2ss2+1s−1)=(−1−(t−2)+e(t−2))u(t−2)\begin{aligned} \mathcal{L}^{-1}\left\{\frac{e^{-2 s}}{s^{2}(s-1)}\right\} &=\mathcal{L}^{-1}\left(-\frac{e^{-2 s}}{s}-\frac{e^{-2 s}}{s^{2}}+\frac{1}{s-1}\right) \\&=\left(-1-(t-2)+e^{(t-2)}\right) u(t-2)\end{aligned}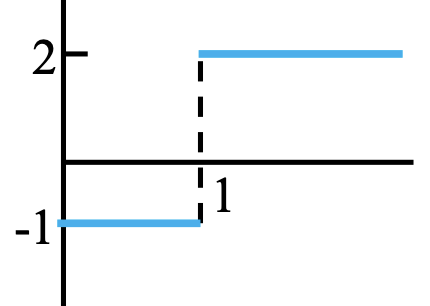

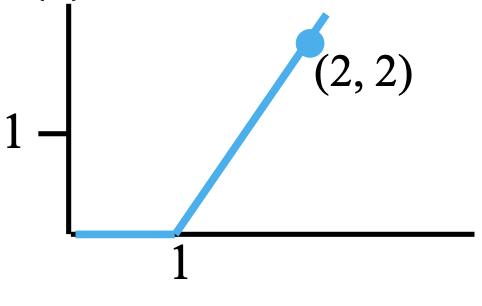
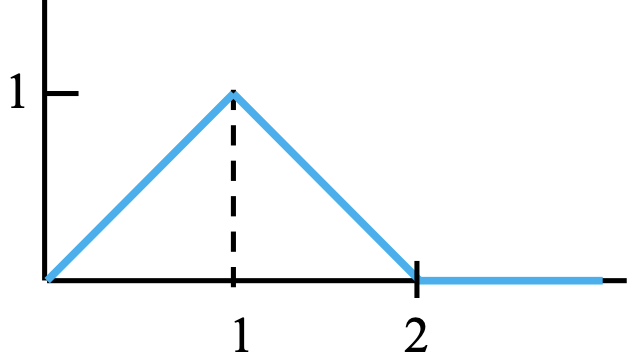
  4. a. Using the Laplace transform definition, evaluate the Laplace transform for the following function:

    b. Prove your answer in part (a) by expressing the functions using unit step function and find L{f(t)}\mathcal{L}\{f(t)\} by referring to the Laplace transform table.

    Solution

    a.

    f(t)={t2,0<t<11,1<t<30,t>3f(t)=\left\{\begin{array}{c}t^{2}, 0<t<1 \\ 1,1<t<3 \\ 0, \quad t>3\end{array}\right.L{f(t)}=∫01t2e−stdt+∫13e−stdt=−1st2e−st∣01+2s∫01te−stdt−1se−st∣13=−1se−s+2s[−tse−st]01+2s2∫01e−stdt−1se−3s+1se−s=2s2e−s+2s2[−1se−st]01−1se−3s=−2s2e−s−2s3e−s+2s3−1se−3s‾‾\begin{aligned}\mathcal{L}\{f(t)\}&=\int_{0}^{1} t^{2} e^{-s t} d t+\int_{1}^{3} e^{-s t} d t\\&=-\left.\frac{1}{s} t^{2} e^{-s t}\right|_{0} ^{1}+\frac{2}{s} \int_{0}^{1} t e^{-s t} d t-\left.\frac{1}{s} e^{-s t}\right|_{1} ^{3}\\&=-\frac{1}{s} e^{-s}+\frac{2}{s}\left[-\frac{t}{s} e^{-s t}\right]_{0}^{1}+\frac{2}{s^{2}} \int_{0}^{1} e^{-s t} d t-\frac{1}{s} e^{-3 s}+\frac{1}{s} e^{-s}\\&=\frac{2}{s^{2}} e^{-s}+\frac{2}{s^{2}}\left[-\frac{1}{s} e^{-s t}\right]_{0}^{1}-\frac{1}{s} e^{-3 s}\\&=\underline{\underline{-\frac{2}{s^{2}} e^{-s}-\frac{2}{s^{3}} e^{-s}+\frac{2}{s^{3}}-\frac{1}{s} e^{-3 s}}}\end{aligned}

    b.

    f(t)=t2(u(t)−u(t−1))+1(u(t−1)−u(t−3))=t2u(t)+(1−t2)u(t−1)−u(t−3)=t2u(t)+(1−(t−1)2−2t+1)u(t−1)−u(t−3)=t2u(t)+(t−1)2u(t−1)−2(t−1)u(t−1)−u(t−3)\begin{aligned}f(t)&=t^{2}(u(t)-u(t-1))+1(u(t-1)-u(t-3))\\&=t^{2} u(t)+\left(1-t^{2}\right) u(t-1)-u(t-3)\\&=t^{2} u(t)+\left(1-(t-1)^{2}-2 t+1\right) u(t-1)-u(t-3)\\&=t^{2} u(t)+(t-1)^{2} u(t-1)-2(t-1) u(t-1)-u(t-3)\end{aligned}L{f(t)}=2s3−2s3e−s−2s2e−s−1se−3s‾‾\mathcal{L}\{f(t)\}=\underline{\underline{\frac{2}{s^{3}}-\frac{2}{s^{3}} e^{-s}-\frac{2}{s^{2}} e^{-s}-\frac{1}{s} e^{-3 s}}}

  5. Using the theorem L{∫0tf(τ)dτ}=1sF(s)\mathcal{L}\left\{\int_0^tf(\tau)d\tau\right\}=\frac{1}{s}F(s), find f(t)f(t) if L{f(t)}=s+1s3+9s\mathcal{L}\{f(t)\}=\frac{s+1}{s^3+9s}. You are not allowed to use partial fraction expansion.

    Solution
    L{f(t)}=s+1s3+9s=s+1s(s2+9)=1sF(s)\mathcal{L}\{f(t)\}=\frac{s+1}{s^{3}+9 s}=\frac{s+1}{s\left(s^{2}+9\right)}=\frac{1}{s} F(s)F(s)=s+1s2+9=ss2+9+1s2+9F(s)=\frac{s+1}{s^{2}+9}=\frac{s}{s^{2}+9}+\frac{1}{s^{2}+9}L−1{ss2+9+1s2+9}=cos⁡3t+13sin⁡3t\mathcal{L}^{-1}\left\{\frac{s}{s^{2}+9}+\frac{1}{s^{2}+9}\right\}=\cos 3 t+\frac{1}{3} \sin 3 tf(t)=L−1{s+1s3+9s}=L−1{1sF(s)}=∫0tf(τ)dτ=∫0tcos⁡3τ+13sin⁡3τdτ=13sin⁡3t−19cos⁡3t+19‾‾\begin{aligned}f(t)=\mathcal{L}^{-1}\left\{\frac{s+1}{s^{3}+9 s}\right\}&=\mathcal{L}^{-1}\left\{\frac{1}{s} F(s)\right\}\\ &=\int_{0}^{t} f(\tau) d \tau\\&=\int_{0}^{t} \cos 3 \tau+\frac{1}{3} \sin 3 \tau d \tau\\&=\underline{\underline{\frac{1}{3} \sin 3 t-\frac{1}{9} \cos 3 t+\frac{1}{9}}}\end{aligned}