Skip to main content

Tutorial 12: Partial Differential Equation I

Tutorial Question

  1. Categorize the following equations in terms of its order, linearity, and homogeneity.

    a. ∂u(x,t)∂t−∂2u(x,t)∂x2+1=0\frac{\partial u(x, t)}{\partial t}-\frac{\partial^2 u(x, t)}{\partial x^2}+1=0

    b. ∂2u∂x∂y−∂u∂y+xu=0\frac{\partial^2 u}{\partial x \partial y}-\frac{\partial u}{\partial y}+x u=0

    c. (utt)3−uxx+x2=0\left(u_{t t}\right)^3-u_{x x}+x^2=0

    d. ux−uxxy+uuy=0u_x-u_{x x y}+u u_y=0

    e. u′+u′′′′+1+u=0u^{\prime}+u^{\prime \prime \prime \prime}+\sqrt{1+u}=0

    Solution

    a. Second order, linear, and non-homogeneous.

    b. Second order, linear, and homogeneous.

    c. Second order, non-linear, and non-homogeneous.

    d. Third order, non-linear, and homogeneous.

    e. Fourth order, non-linear, and non-homogeneous

Classify the category of the following PDEs and solve the PDEs using separation of variable method.

  1. uxx+uyy=0u_{x x}+u_{y y}=0

    Solution

    General form: A∂2u∂x2+B∂2u∂x∂t+C∂2u∂t2+D∂u∂x+E∂u∂t+Fu=0A \frac{\partial^2 u}{\partial x^2}+B \frac{\partial^2 u}{\partial x \partial t}+C \frac{\partial^2 u}{\partial t^2}+D \frac{\partial u}{\partial x}+E \frac{\partial u}{\partial t}+F u=0

    A=1, B=0,C=1,B2−4AC=0−4(1)(1)<0\mathrm{A}=1, \mathrm{~B}=0, \mathrm{C}=1, B^2-4 A C=0-4(1)(1)<0, Elliptic PDE

    Step 1: Let u(x,y)=X(x)Y(y)u(x, y)=X(x) Y(y)

    ∂2u∂x2+∂2u∂y2=0X′′Y+XY′′=0\begin{aligned} \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}&=0 \\ X^{\prime \prime} Y+X Y^{\prime \prime}&=0 \end{aligned}

    Step 2: Obtain 2 ODE equations

    X′′X=−Y′′Y=−λX′′+λX=0;Y′′−λY=0\begin{aligned} \frac{X^{\prime \prime}}{X}&=-\frac{Y^{\prime \prime}}{Y}=-\lambda \\ X^{\prime \prime}+\lambda X&=0 ; \quad Y^{\prime \prime}-\lambda Y=0 \end{aligned}

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    Y′′=0\boldsymbol{Y}^{\prime \prime}=\mathbf{0}X′′=0X^{\prime \prime}=\mathbf{0}
    Let Y(x)=eryY(x)=e^{r y}
    Characteristic equation: r2=0r^{2}=0
    Y(y)=c1e0y+c2ye0yY(y)=c_{1} e^{0 y}+c_{2} y e^{0 y}
    ∴Y(y)=c1+c2y\therefore Y(y)=c_{1}+c_{2} y    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c3e0x+c4xe0xX(x)=c_{3} e^{0 x}+c_{4} x e^{0 x}
    ∴X(x)=c3+c4x\therefore X(x)=c_{3}+c_{4} x

    ∴u1=X1(x)Y1(y)=(c1+c2y)(c3+c4x)\therefore u_{1}=X_{1}(x) Y_{1}(y)=\left(c_{1}+c_{2} y\right)\left(c_{3}+c_{4} x\right)

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    Y′′+α2Y=0\boldsymbol{Y}^{\prime \prime}+\boldsymbol{\alpha}^{2} \boldsymbol{Y}=\mathbf{0}X′′−α2X=0\boldsymbol{X}^{\prime \prime}-\boldsymbol{\alpha}^{2} \boldsymbol{X}=\mathbf{0}
    Let Y(y)=eryY(y)=e^{r y}
    Characteristic equation:
    r2+α2=0r=±−α2r=+αi,−αi\begin{aligned}r^{2}+\alpha^{2}&=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴Y(y)=c5cos⁡(αy)+c6sin⁡(αy)\therefore Y(y)=c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned}r^{2}-\alpha^{2}&=0 \\ r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴X(x)=c7cosh⁡(αx)+c8sinh⁡(αx)\therefore X(x)=c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)

    ∴u2=X2(x)Y2(y)=(c5cos⁡(αy)+c6sin⁡(αy))(c7cosh⁡(αx)+c8sinh⁡(αx))\therefore u_{2}=X_{2}(x) Y_{2}(y)=\left(c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)\right)\left(c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)\right)

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    Y′′−α2Y=0\boldsymbol{Y}^{\prime \prime}-\boldsymbol{\alpha}^{2} \boldsymbol{Y}=\mathbf{0}X′′+α2X=0\boldsymbol{X}^{\prime \prime}+\boldsymbol{\alpha}^{2} \boldsymbol{X}=\mathbf{0}
    Let Y(y)=eryY(y)=e^{r y}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned} r^{2}-\alpha^{2}&=0\\r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴Y(y)=c9cosh⁡(αy)+c10sinh⁡(αy)\therefore Y(y)=c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+α2=0r=±−α2r=+αi,−αi\begin{aligned} r^{2}+\alpha^{2}&=0 \\ r &= \pm \sqrt{-\alpha^{2}} \\ r&=+\alpha i,-\alpha i \end{aligned}
    ∴X(x)=c11cos⁡(αx)+c12sin⁡(αx)\therefore X(x)=c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)

    ∴u3=X3(x)Y3(y)=(c9cosh⁡(αy)+c10sinh⁡(αy))(c11cos⁡(αx)+c12sin⁡(αx))\therefore u_{3}=X_{3}(x) Y_{3}(y)=\left(c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)\right)\left(c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)\right)

    ∴\therefore General solution:

    u(x,y)=u1+u2+u3=(c1+c2y)(c3+c4x)+(c5cos⁡(αy)+c6sin⁡(αy))(c7cosh⁡(αx)+c8sinh⁡(αx))+(c9cosh⁡(αy)+c10sinh⁡(αy))(c11cos⁡(αx)+c12sin⁡(αx))\begin{aligned} u(x, y)&=u_{1}+u_{2}+u_{3}\\ &=\left(c_{1}+c_{2} y\right)\left(c_{3}+c_{4} x\right)+\left(c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)\right)\left(c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)\right)\\ &+\left(c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)\right)\left(c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)\right) \end{aligned}

  2. ut−uxx=0u_t-u_{x x}=0

    Solution

    A=1,B=0,C=0,B2−4AC=0−4(1)(0)=0\mathrm{A}=1, \mathrm{B}=0, \mathrm{C}=0, B^{2}-4 A C=0-4(1)(0)=0, Parabolic PDE

    Step 1: Let u(x,t)=X(x)T(t)u(x, t)=X(x) T(t)

    ∂u∂t−∂2u∂x2=0\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{\partial x^{2}}=0

    XT′−X′′T=0X T^{\prime}-X^{\prime \prime} T=0

    Step 2: Obtain 2 ODE equations

    X′′X=T′T=−λ\frac{X^{\prime \prime}}{X}=\frac{T^{\prime}}{T}=-\lambda

    T′+λT=0;X′′+λX=0T^{\prime}+\lambda T=0 ; \quad X^{\prime \prime}+\lambda X=0

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    T′=0\boldsymbol{T}^{\prime}=\mathbf{0}X′′=0\boldsymbol{X}^{\prime \prime}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation: r=0r=0
    ∴T(t)=c1e0t=c1\therefore T(t)=c_{1} e^{0 t}=c_{1}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c2e0x+c3xe0xX(x)=c_{2} e^{0 x}+c_{3} x e^{0 x}
    ∴X(x)=c2+c3x\therefore X(x)=c_{2}+c_{3} x

    ∴u1=X1(x)T1(t)=(c2+c3x)(c1)=A1x+B1\therefore u_{1}=X_{1}(x) T_{1}(t)=\left(c_{2}+c_{3} x\right)\left(c_{1}\right)=A_{1} x+B_{1} where A1,B1=A_{1}, B_{1}= constant

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    T′−α2T=0\boldsymbol{T}^{\prime} - \boldsymbol{\alpha}^2\boldsymbol{T} =\mathbf{0}X′′−α2X=0\boldsymbol{X}^{\prime \prime} - \boldsymbol{\alpha}^2\boldsymbol{X} =\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation: r−α2=0r-\alpha^{2}=0
    r=α2r=\alpha^{2}
    ∴T(t)=c4eα2t\therefore T(t)=c_{4} e^{\alpha^{2} t}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2−α2=0r^{2}-\alpha^{2}=0
    r=±α2r=+α,−α\begin{aligned} r&= \pm \sqrt{\alpha^{2}} \\ r&=+\alpha,-\alpha \end{aligned}
    ∴X(x)=c5cosh⁡(αx)+c6sinh⁡(αx)\therefore X(x)=c_{5} \cosh (\alpha x)+c_{6} \sinh (\alpha x)

    ∴u2=X2(x)T2(t)=eα2t(A2cosh⁡(αx)+B2sinh⁡(αx))\therefore u_{2}=X_{2}(x) T_{2}(t)=e^{\alpha^{2} t}\left(A_{2} \cosh (\alpha x)+B_{2} \sinh (\alpha x)\right) where A2,B2=A_{2}, B_{2}= constant

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    T′+α2T=0\boldsymbol{T}^{\prime} + \boldsymbol{\alpha}^2\boldsymbol{T} =\mathbf{0}X′′+α2X=0\boldsymbol{X}^{\prime \prime} + \boldsymbol{\alpha}^2\boldsymbol{X} =\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r+α2=0r=−α2\begin{aligned}r+\alpha^{2}&=0\\r&=-\alpha^{2}\end{aligned}
    ∴T(t)=c7e−α2t\therefore T(t)=c_{7} e^{-\alpha^{2} t}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+α2=0r=±−α2r=+αi,−αi\begin{aligned}r^{2}+\alpha^{2}&=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴X(x)=c8cos⁡(αx)+c9sin⁡(αx)\therefore X(x)=c_{8} \cos (\alpha x)+c_{9} \sin (\alpha x)

    ∴u3=X3(x)T3(t)=e−α2t(A3cos⁡(αx)+B3sin⁡(αx))\therefore u_{3}=X_{3}(x) T_{3}(t)=e^{-\alpha^{2} t}\left(A_{3} \cos (\alpha x)+B_{3} \sin (\alpha x)\right) where A3,B3=A_{3}, B_{3}= constant

    ∴\therefore General solution:

    u(x,t)=u1+u2+u3=A1x+B1+eα2t(A2cosh⁡(αx)+B2sinh⁡(αx))+e−α2t(A3cos⁡(αx)+B3sin⁡(αx))\begin{aligned} u(x, t)&=u_{1}+u_{2}+u_{3}\\ &=A_{1} x+B_{1}+e^{\alpha^{2} t}\left(A_{2} \cosh (\alpha x)+B_{2} \sinh (\alpha x)\right)+e^{-\alpha^{2} t}\left(A_{3} \cos (\alpha x)+B_{3} \sin (\alpha x)\right) \end{aligned}

  3. ut−116uxx=0u_t-\frac{1}{16} u_{x x}=0

    Solution

    A=−116, B=0,C=0,B2−4AC=0−4(−116)(0)=0\mathrm{A}=-\frac{1}{16}, \mathrm{~B}=0, \mathrm{C}=0, B^{2}-4 A C=0-4\left(-\frac{1}{16}\right)(0)=0, Parabolic PDE

    Step 1: Let u(x,t)=X(x)T(t)u(x, t)=X(x) T(t)

    ∂u∂t−∂2u16∂x2=0\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{16 \partial x^{2}}=0

    XT′−116X′′T=0X T^{\prime}-\frac{1}{16} X^{\prime \prime} T=0

    Step 2: Obtain 2 ODE equations

    X′′16X=T′T=−λT′+λT=0;X′′+16λX=0\begin{aligned} & \frac{X^{\prime \prime}}{16 X}=\frac{T^{\prime}}{T}=-\lambda \\ & T^{\prime}+\lambda T=0 ; \quad X^{\prime \prime}+16 \lambda X=0 \end{aligned}

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    T′=0\boldsymbol{T}^{\prime}=\mathbf{0}X′′=0\boldsymbol{X}^{\prime \prime}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation: r=0r=0
    ∴T(t)=c1e0t=c1\therefore T(t)=c_{1} e^{0 t}=c_{1}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c2e0x+c3xe0xX(x)=c_{2} e^{0 x}+c_{3} x e^{0 x}
    ∴X(x)=c2+c3x\therefore X(x)=c_{2}+c_{3} x

    ∴u1=X1(x)T1(t)=(c2+c3x)(c1)=A1x+B1 where A1,B1= constant \therefore u_{1}=X_{1}(x) T_{1}(t)=\left(c_{2}+c_{3} x\right)\left(c_{1}\right)=A_{1} x+B_{1} \text { where } A_{1}, B_{1}=\text { constant }

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    T′−α2T=0\boldsymbol{T}^{\prime}-\boldsymbol{\alpha}^2\boldsymbol{T}=\mathbf{0}X′′−16α2X=0\boldsymbol{X}^{\prime \prime}-\mathbf{16}\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r−α2=0r=α2\begin{aligned}r-\alpha^{2}&=0 \\ r&=\alpha^{2}\end{aligned}
    ∴T(t)=c4eα2t\therefore T(t)=c_{4} e^{\alpha^{2} t}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2−16α2=0r=±16α2r=+4α,−4α\begin{aligned}r^{2}-16 \alpha^{2}&=0\\r&= \pm \sqrt{16 \alpha^{2}}\\r&=+4 \alpha,-4 \alpha\end{aligned}
    ∴X(x)=c5cosh⁡(4αx)+c6sinh⁡(4αx)\therefore X(x)=c_{5} \cosh (4 \alpha x)+c_{6} \sinh (4 \alpha x)

    ∴u2=X2(x)T2(t)=eα2t(A2cosh⁡(4αx)+B2sinh⁡(4αx))\therefore u_{2}=X_{2}(x) T_{2}(t)=e^{\alpha^{2} t}\left(A_{2} \cosh (4 \alpha x)+B_{2} \sinh (4 \alpha x)\right) where A2,B2=A_{2}, B_{2}= constant

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    T′+α2T=0\boldsymbol{T}^{\prime}+\boldsymbol{\alpha}^2\boldsymbol{T}=\mathbf{0}X′′+16α2X=0\boldsymbol{X}^{\prime \prime}+\mathbf{16}\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r+α2=0r=−α2\begin{aligned} r+\alpha^{2}&=0 \\ r&=-\alpha^{2}\end{aligned}
    ∴T(t)=c7e−α2t\therefore T(t)=c_{7} e^{-\alpha^{2} t}    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+16α2=0r=±−16α2r=+4αi,−4αi\begin{aligned}r^{2}+16 \alpha^{2}&=0 \\ r&= \pm \sqrt{-16 \alpha^{2}} \\ r&=+4 \alpha i,-4 \alpha i \end{aligned}
    ∴X(x)=c8cos⁡(4αx)+c9sin⁡(4αx)\therefore X(x)=c_{8} \cos (4 \alpha x)+c_{9} \sin (4 \alpha x)

    ∴u3=X3(x)T3(t)=e−α2t(A3cos⁡(4αx)+B3sin⁡(4αx)) where A3,B3= constant \therefore u_{3}=X_{3}(x) T_{3}(t)=e^{-\alpha^{2} t}\left(A_{3} \cos (4 \alpha x)+B_{3} \sin (4 \alpha x)\right) \text { where } A_{3}, B_{3}=\text { constant }

    ∴\therefore General solution:

    u(x,t)=u1+u2+u3=A1x+B1+eα2t(A2cosh⁡(4αx)+B2sinh⁡(4αx))+e−α2t(A3cos⁡(4αx)+B3sin⁡(4αx))\begin{aligned} u(x, t)&=u_{1}+u_{2}+u_{3} \\ &=A_{1} x+B_{1}+e^{\alpha^{2} t}\left(A_{2} \cosh (4 \alpha x)+B_{2} \sinh (4 \alpha x)\right)+e^{-\alpha^{2} t}\left(A_{3} \cos (4 \alpha x)+B_{3} \sin (4 \alpha x)\right) \end{aligned}

  4. utt−uxx=0u_{t t}-u_{x x}=0

    Solution

    A=−1, B=0,C=1,B2−4AC=0−4(−1)(1)>0\mathrm{A}=-1, \mathrm{~B}=0, \mathrm{C}=1, B^{2}-4 A C=0-4(-1)(1)>0, Hyperbolic PDE

    Step 1: Let u(x,t)=X(x)T(t)u(x, t)=X(x) T(t)

    ∂2u∂t2−∂2u∂x2=0\frac{\partial^{2} u}{\partial t^{2}}-\frac{\partial^{2} u}{\partial x^{2}}=0

    XT′′−X′′T=0X T^{\prime \prime}-X^{\prime \prime} T=0

    Step 2: Obtain 2 ODE equations

    X′′X=T′′T=−λT′′+λT=0;X′′+λX=0\begin{aligned} & \frac{X^{\prime \prime}}{X}=\frac{T^{\prime \prime}}{T}=-\lambda \\ & T^{\prime \prime}+\lambda T=0 ; \quad X^{\prime \prime}+\lambda X=0 \end{aligned}

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    T′′=0\boldsymbol{T}^{\prime \prime}=\mathbf{0}X′′=0\boldsymbol{X}^{\prime \prime}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation: r2=0r^{2}=0
    T(t)=c1e0t+c2te0tT(t)=c_{1} e^{0 t}+c_{2} t e^{0 t}
    ∴T(t)=c1+c2t\therefore T(t)=c_{1}+c_{2} t    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c3e0x+c4xe0xX(x)=c_{3} e^{0 x}+c_{4} x e^{0 x}
    ∴X(x)=c3+c4x\therefore X(x)=c_{3}+c_{4} x

    ∴u1=X1(x)T1(t)=(c1+c2t)(c3+c4x)\therefore u_{1}=X_{1}(x) T_{1}(t)=\left(c_{1}+c_{2} t\right)\left(c_{3}+c_{4} x\right)

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    T′′−α2T=0\boldsymbol{T}^{\prime \prime}-\boldsymbol{\alpha}^{2} \boldsymbol{T}=\mathbf{0}X′′−α2X=0\boldsymbol{X}^{\prime \prime}-\boldsymbol{\alpha}^{2} \boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned}r^{2}-\alpha^{2}&=0\\r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴T(t)=c5cosh⁡(αt)+c6sinh⁡(αt)\therefore T(t)=c_{5} \cosh (\alpha t)+c_{6} \sinh (\alpha t)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned}r^{2}-\alpha^{2}&=0\\r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴X(x)=c7cosh⁡(αx)+c8sinh⁡(αx)\therefore X(x)=c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)

    ∴u2=X2(x)T2(t)=(c5cosh⁡(αt)+c6sinh⁡(αt))(c7cosh⁡(αx)+c8sinh⁡(αx))\therefore u_{2}=X_{2}(x) T_{2}(t)=\left(c_{5} \cosh (\alpha t)+c_{6} \sinh (\alpha t)\right)\left(c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)\right)

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    T′′+α2T=0\boldsymbol{T}^{\prime \prime}+\boldsymbol{\alpha}^{2} \boldsymbol{T}=\mathbf{0}X′′+α2X=0\boldsymbol{X}^{\prime \prime}+\boldsymbol{\alpha}^{2} \boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r+α2=0r=±−α2r=+αi,−αi\begin{aligned}r+\alpha^{2}&=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴T(t)=c9cos⁡(αt)+c10sin⁡(αt)\therefore T(t)=c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+α2=0r=±−α2r=+αi,−αi\begin{aligned}r^{2}+\alpha^{2}&=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴X(x)=c11cos⁡(αx)+c12sin⁡(αx)\therefore X(x)=c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)

    ∴u3=X3(x)T3(t)=(c9cos⁡(αt)+c10sin⁡(αt))(c11cos⁡(αx)+c12sin⁡(αx))\therefore u_{3}=X_{3}(x) T_{3}(t)=\left(c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)\right)\left(c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)\right)

    ∴\therefore General solution:

    u(x,t)=u1+u2+u3=(c1+c2t)(c3+c4x)+(c5cosh⁡(αt)+c6sinh⁡(αt))(c7cosh⁡(αx)+c8sinh⁡(αx))+(c9cos⁡(αt)+c10sin⁡(αt))(c11cos⁡(αx)+c12sin⁡(αx))\begin{aligned} u(x, t)&=u_{1}+u_{2}+u_{3}\\ &=\left(c_{1}+c_{2} t\right)\left(c_{3}+c_{4} x\right)+\left(c_{5} \cosh (\alpha t)+c_{6} \sinh (\alpha t)\right)\left(c_{7} \cosh (\alpha x)+c_{8} \sinh (\alpha x)\right) \\ &+\left(c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)\right)\left(c_{11} \cos (\alpha x)+c_{12} \sin (\alpha x)\right) \end{aligned}

  5. uxx=3uyyu_{x x}=3 u_{y y}

    Solution

    A=1, B=0,C=3,B2−4AC=0−4(1)(3)<0\mathrm{A}=1, \mathrm{~B}=0, \mathrm{C}=3, B^{2}-4 A C=0-4(1)(3)<0, Elliptic PDE

    Step 1: Let u(x,y)=X(x)Y(y)u(x, y)=X(x) Y(y)

    ∂2u∂x2+3∂2u∂y2=0\frac{\partial^{2} u}{\partial x^{2}}+3 \frac{\partial^{2} u}{\partial y^{2}}=0

    X′′Y+3XY′′=0X^{\prime \prime} Y+3 X Y^{\prime \prime}=0

    Step 2: Obtain 2 ODE equations

    X′′3X=−Y′′Y=−λX′′+3λX=0;Y′′−λY=0\begin{aligned} & \frac{X^{\prime \prime}}{3 X}=-\frac{Y^{\prime \prime}}{Y}=-\lambda \\ & X^{\prime \prime}+3 \lambda X=0 ; \quad Y^{\prime \prime}-\lambda Y=0 \end{aligned}

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    Y′′=0\boldsymbol{Y}^{\prime \prime}=\mathbf{0}X′′=0\boldsymbol{X}^{\prime \prime}=\mathbf{0}
    Let Y(x)=eryY(x)=e^{r y}
    Characteristic equation: r2=0r^{2}=0
    Y(y)=c1e0y+c2ye0yY(y)=c_{1} e^{0 y}+c_{2} y e^{0 y}
    ∴Y(y)=c1+c2y\therefore Y(y)=c_{1}+c_{2} y    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c3e0x+c4xe0xX(x)=c_{3} e^{0 x}+c_{4} x e^{0 x}
    ∴X(x)=c3+c4x\therefore X(x)=c_{3}+c_{4} x

    ∴u1=X1(x)Y1(y)=(c1+c2y)(c3+c4x)\therefore u_{1}=X_{1}(x) Y_{1}(y)=\left(c_{1}+c_{2} y\right)\left(c_{3}+c_{4} x\right)

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    Y′′+α2Y=0\boldsymbol{Y}^{\prime \prime}+\boldsymbol{\alpha}^2\boldsymbol{Y}=\mathbf{0}X′′−3α2X=0\boldsymbol{X}^{\prime \prime}-\mathbf{3}\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let Y(y)=eryY(y)=e^{r y}
    Characteristic equation:
    r2+α2=0r=±−α2r=+αi,−αi\begin{aligned}r^{2}+\alpha^{2}&=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴:Y(y)=c5cos⁡(αy)+c6sin⁡(αy)\therefore: Y(y)=c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2−3α2=0r=±3α2r=+3α,−3α\begin{aligned}r^{2}-3 \alpha^{2}&=0\\r&= \pm \sqrt{3 \alpha^{2}}\\r&=+\sqrt{3} \alpha,-\sqrt{3} \alpha\end{aligned}
    ∴X(x)=c7cosh⁡(3αx)+c8sinh⁡(3αx)\therefore X(x)=c_{7} \cosh (\sqrt{3} \alpha x)+c_{8} \sinh (\sqrt{3} \alpha x)

    ∴u2=X2(x)Y2(y)=(c5cos⁡(αy)+c6sin⁡(αy))(c7cosh⁡(3αx)+c8sinh⁡(3αx))\therefore u_{2}=X_{2}(x) Y_{2}(y)=\left(c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)\right)\left(c_{7} \cosh (\sqrt{3} \alpha x)+c_{8} \sinh (\sqrt{3} \alpha x)\right)

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    Y′′−α2Y=0\boldsymbol{Y}^{\prime \prime}-\boldsymbol{\alpha}^2\boldsymbol{Y}=\mathbf{0}X′′+3α2X=0\boldsymbol{X}^{\prime \prime}+\mathbf{3}\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let Y(y)=eryY(y)=e^{r y}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned}r^{2}-\alpha^{2}&=0\\r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴Y(y)=c9cosh⁡(αy)+c10sinh⁡(αy)\therefore Y(y)=c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+α2=0r=±−3α2r=+3αi,−3αi\begin{aligned}r^{2}+\alpha^{2}&=0\\r&= \pm \sqrt{-3 \alpha^{2}}\\r&=+\sqrt{3} \alpha i,-\sqrt{3} \alpha i\end{aligned}
    ∴X(x)=c11cos⁡(3αx)+c12sin⁡(3αx)\therefore X(x)=c_{11} \cos (\sqrt{3} \alpha x)+c_{12} \sin (\sqrt{3} \alpha x)

    ∴u3=X3(x)Y3(y)=(c9cosh⁡(αy)+c10sinh⁡(αy))(c11cos⁡(3αx)+c12sin⁡(3αx))\therefore u_{3}=X_{3}(x) Y_{3}(y)=\left(c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)\right)\left(c_{11} \cos (\sqrt{3} \alpha x)+c_{12} \sin (\sqrt{3} \alpha x)\right)

    ∴\therefore General solution:

    u(x,y)=u1+u2+u3=(c1+c2y)(c3+c4x)+(c5cos⁡(αy)+c6sin⁡(αy))(c7cosh⁡(3αx)+c8sinh⁡(3αx))+(c9cosh⁡(αy)+c10sinh⁡(αy))(c11cos⁡(3αx)+c12sin⁡(3αx))\begin{aligned} u(x, y)&=u_{1}+u_{2}+u_{3}\\ &=\left(c_{1}+c_{2} y\right)\left(c_{3}+c_{4} x\right)+\left(c_{5} \cos (\alpha y)+c_{6} \sin (\alpha y)\right)\left(c_{7} \cosh (\sqrt{3} \alpha x)+c_{8} \sinh (\sqrt{3} \alpha x)\right)\\ &+\left(c_{9} \cosh (\alpha y)+c_{10} \sinh (\alpha y)\right)\left(c_{11} \cos (\sqrt{3} \alpha x)+c_{12} \sin (\sqrt{3} \alpha x)\right) \end{aligned}

  6. utt=4a2uxxu_{t t}=4 a^2 u_{x x}

    Solution

    A=4a2, B=0,C=−1,B2−4AC=0−4(4a2)(−1)>0\mathrm{A}=4 a^{2}, \mathrm{~B}=0, \mathrm{C}=-1, B^{2}-4 A C=0-4\left(4 a^{2}\right)(-1)>0, Hyperbolic PDE

    Step 1: Let u(x,t)=X(x)T(t)u(x, t)=X(x) T(t)

    ∂2u∂t2−4a2∂2u∂x2=0\frac{\partial^{2} u}{\partial t^{2}}-4 a^{2} \frac{\partial^{2} u}{\partial x^{2}}=0

    XT′′−4a2X′′T=0X T^{\prime \prime}-4 a^{2} X^{\prime \prime} T=0

    Step 2: Obtain 2 ODE equations

    X′′4a2X=T′′T=−λT′′+λT=0;X′′+4a2λX=0\begin{aligned} & \frac{X^{\prime \prime}}{4 a^{2} X}=\frac{T^{\prime \prime}}{T}=-\lambda \\ & T^{\prime \prime}+\lambda T=0 ; \quad X^{\prime \prime}+4 a^{2} \lambda X=0 \end{aligned}

    Step 3: 3 cases

    Case 1, λ=0\lambda=0

    T′′=0\boldsymbol{T}^{\prime \prime}=\mathbf{0}X′′=0\boldsymbol{X}^{\prime \prime}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation: r2=0r^{2}=0
    T(t)=c1e0t+c2te0tT(t)=c_{1} e^{0 t}+c_{2} t e^{0 t}
    ∴T(t)=c1+c2t\therefore T(t)=c_{1}+c_{2} t    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation: r2=0r^{2}=0
    X(x)=c3e0x+c4xe0xX(x)=c_{3} e^{0 x}+c_{4} x e^{0 x}
    ∴X(x)=c3+c4x\therefore X(x)=c_{3}+c_{4} x

    ∴u1=X1(x)T1(t)=(c1+c2t)(c3+c4x)\quad \therefore u_{1}=X_{1}(x) T_{1}(t)=\left(c_{1}+c_{2} t\right)\left(c_{3}+c_{4} x\right)

    Case 2, λ=−α2,α>0\lambda=-\alpha^{2}, \alpha>0

    T′′−α2T=0\boldsymbol{T}^{\prime \prime}-\boldsymbol{\alpha}^2\boldsymbol{T}=\mathbf{0}X′′−4α2α2X=0\boldsymbol{X}^{\prime \prime}-\mathbf{4}\boldsymbol{\alpha}^2\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r2−α2=0r=±α2r=+α,−α\begin{aligned}r^{2}-\alpha^{2}&=0\\r&= \pm \sqrt{\alpha^{2}}\\r&=+\alpha,-\alpha\end{aligned}
    ∴T(t)=c5cosh⁡(αt)+c6sinh⁡(αt)\therefore T(t)=c_{5} \cosh (\alpha t)+c_{6} \sinh (\alpha t)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2−4a2α2=0r=±4a2α2r=+2aα,−2aα\begin{aligned}r^{2}-4 a^{2} \alpha^{2}&=0\\r&= \pm \sqrt{4 a^{2} \alpha^{2}}\\r&=+2 a \alpha,-2 a \alpha\end{aligned}
    ∴X(x)=c7cosh⁡(2aαx)+c8sinh⁡(2aαx)\therefore X(x)=c_{7} \cosh (2 a \alpha x)+c_{8} \sinh (2 a \alpha x)

    ∴u2=X2(x)T2(t)=(c5cosh⁡(αt)+c6sinh⁡(αt))(c7cosh⁡(2aαx)+c8sinh⁡(2aαx))\therefore u_{2}=X_{2}(x) T_{2}(t)=\left(c_{5} \cosh (\alpha t)+c_{6} \sinh (\alpha t)\right)\left(c_{7} \cosh (2 a \alpha x)+c_{8} \sinh (2 a \alpha x)\right)

    Case 3, λ=+α2,α>0\lambda=+\alpha^{2}, \alpha>0

    T′′+α2T=0\boldsymbol{T}^{\prime \prime}+\boldsymbol{\alpha}^2\boldsymbol{T}=\mathbf{0}X′′+4α2α2X=0\boldsymbol{X}^{\prime \prime}+\mathbf{4}\boldsymbol{\alpha}^2\boldsymbol{\alpha}^2\boldsymbol{X}=\mathbf{0}
    Let T(t)=ertT(t)=e^{r t}
    Characteristic equation:
    r+α2=0r=±−α2r=+αi,−αi\begin{aligned}r+\alpha^{2}=0\\r&= \pm \sqrt{-\alpha^{2}}\\r&=+\alpha i,-\alpha i\end{aligned}
    ∴T(t)=c9cos⁡(αt)+c10sin⁡(αt)\therefore T(t)=c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)    		Let X(x)=erxX(x)=e^{r x}
    Characteristic equation:
    r2+4a2α2=0r=±−4a2α2r=+2ααi,−2ααi\begin{aligned} r^{2}+4 a^{2} \alpha^{2}&=0 \\ r&= \pm \sqrt{-4 a^{2} \alpha^{2}} \\ r&=+2 \alpha \alpha i,-2 \alpha \alpha i\end{aligned}
    ∴X(x)=c11cos⁡(2ααx)+c12sin⁡(2ααx)\therefore X(x)=c_{11} \cos (2 \alpha \alpha x)+c_{12} \sin (2 \alpha \alpha x)

    ∴u3=X3(x)T3(t)=(c9cos⁡(αt)+c10sin⁡(αt))(c11cos⁡(2ααx)+c12sin⁡(2ααx))\therefore u_{3}=X_{3}(x) T_{3}(t)=\left(c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)\right)\left(c_{11} \cos (2 \alpha \alpha x)+c_{12} \sin (2 \alpha \alpha x)\right)

    ∴\therefore General solution:

    u(x,t)=u1+u2+u3=(c1+c2t)(c3+c4x)+(c5cos⁡h(αt)+c6sinh⁡(αt))(c7cos⁡h(2ααx)+c8sinh⁡(2ααx)+(c9cos⁡(αt)+c10sin⁡(αt))(c11cos⁡(2ααx)+c12sin⁡(2ααx))\begin{aligned} u(x, t)&=u_{1}+u_{2}+u_{3} \\ &=\left(c_{1}+c_{2} t\right)\left(c_{3}+c_{4} x\right)+\left(c_{5} \cos h(\alpha t)+c_{6} \sinh (\alpha t)\right)\left(c_{7} \cos h(2 \alpha \alpha x)+c_{8} \sinh (2 \alpha \alpha x)\right. \\ &+\left(c_{9} \cos (\alpha t)+c_{10} \sin (\alpha t)\right)\left(c_{11} \cos (2 \alpha \alpha x)+c_{12} \sin (2 \alpha \alpha x)\right) \end{aligned}

  7. Set up the boundary and initial conditions from the given statement/figure that describe the scenario. Consider a hot place of area (xyxy), set up the boundary value problem for the steady-state temperature over the xx and yy location, i.e. u(x,y)u(x,y).

    ∂2u∂x2+∂2u∂y2=0\frac{\partial^2 u}{\partial x^2}+ \frac{\partial^2 u}{\partial y^2}=0
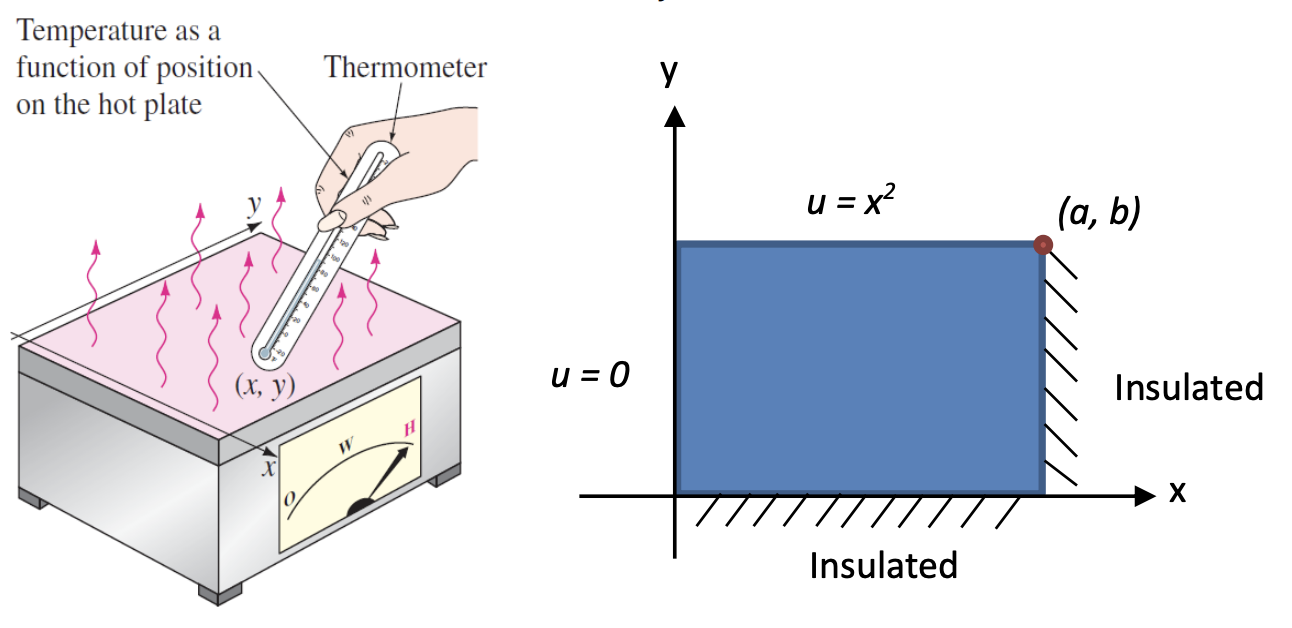    Solution

    ∂2u∂x2+∂2u∂y2=0\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0 for 0<x<a,0<y<b0<x<a, 0<y<b

    Boundary condition:

    u(0,y)=0,∂u∂x∣x=a=0u(0, y)=0,\left.\frac{\partial u}{\partial x}\right|_{x=a}=0 for 0<y<b0<y<b

    u(x,b)=x2,∂u∂y∣y=0=0u(x, b)=x^2,\left.\frac{\partial u}{\partial y}\right|_{y=0}=0 for 0<x<a0<x<a

  8. Set up the boundary and initial conditions from the given statement/figure that describe the scenario. A metal rod coincides with the interval [0,L][0, L] on the x-axis with both ends fixed at 0 ̊C. It has an initial temperature of cos⁡(πLx)\cos\left(\frac{\pi}{L} x\right). Set up the boundary value problem for the temperature u(x,t)u(x, t).

    k∂2u∂x2=∂u∂tk\frac{\partial^2 u}{\partial x^2}=\frac{\partial u}{\partial t}
    Solution

    k∂2u∂x2=∂u∂tk \frac{\partial^2 u}{\partial x^2}=\frac{\partial u}{\partial t} for 0<x<L,t>00<x<L, \quad t>0

    Boundary condition: u(0,t)=0,u(L,t)=0u(0, t)=0, u(L, \mathrm{t})=0 \quad for t>0t>0

    Initial condition: u(x,0)=cos⁡(πLx)\quad u(x, 0)=\cos \left(\frac{\pi}{L} x\right) \quad for 0<x<L0<x<L

  9. Set up the boundary value problem for the displacement u(x,t)u(x, t) when a string with length, L=1L = 1, is fixed at the two ends on the x-axis with the initial shape shown as the graph below. The string is released from rest.

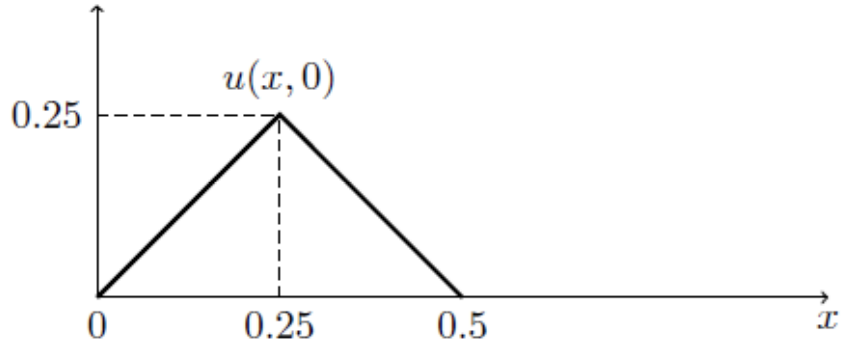    α2∂2u∂x2=∂2u∂t2\alpha^2\frac{\partial^2 u}{\partial x^2}=\frac{\partial^2 u}{\partial t^2}
    Solution

    a2∂2u∂x2=∂2u∂t2a^2 \frac{\partial^2 u}{\partial x^2}=\frac{\partial^2 u}{\partial t^2} for 0<x<1,t>00<x<1, \quad t>0

    Boundary condition: u(0,0)=0,u(L,0)=0u(0,0)=0, u(L, 0)=0

    Initial condition: u(x,0)=f(x)={x for 0<x<1412−x for 14<x<120 for 12<x<1u(x, 0)=f(x)=\left\{\begin{array}{cl}x & \text { for } 0<x<\frac{1}{4} \\ \frac{1}{2}-x & \text { for } \frac{1}{4}<x<\frac{1}{2} \\ 0 & \text { for } \frac{1}{2}<x<1\end{array}\right.

    ut(x,0)=0u_t(x, 0)=0

  10. Match the given situations to their corresponding equations and conditions.

    SituationEquationCondition
    (a)

    uy(x,0)−u(x,0)=f(x)u_y(x,0)-u(x,0)=f(x)    		(d)
    1D Heat Equation
    ∂u∂t=c2∂2u∂x2\frac{\partial u}{\partial t} = c^2 \frac{\partial^2 u}{\partial x^2}    		(g)
    −∞<x<∞-\infty<x<\infty
    y>0y>0
    ∂u(x,0)∂y−u(x,0)=f(x)\frac{\partial u(x,0)}{\partial y}-u(x,0)=f(x)
    (b)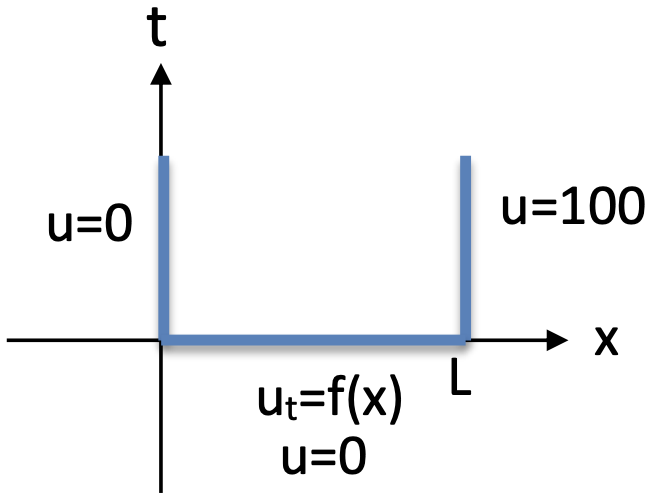
    		(e)
    2D Laplace Equation
    ∂2u∂x2+∂2u∂y2=0\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0    		(h)
    u(0,t)=100,t>0u(0, t)=100, t>0
    u(x,0)=0,0<x<Lu(x, 0)=0,0<x<L
    ∂u∂x∣x=L=f(x),t>0\left.\frac{\partial u}{\partial x}\right\vert_{x=L}=f(x), t>0
    (c)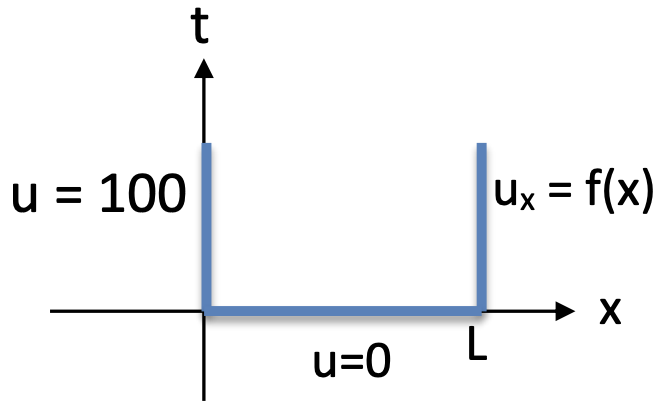
    		(f)
    1D Wave Equation
    ∂2u∂t2=c2∂2u∂x2\frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2 u}{\partial x^2}    		(i)
    u(0,t)=0u(L,t)=100}t>0\left.\begin{array}{c} u(0, t)=0 \\ u(L, t)=100 \end{array}\right\} t>0
    u(x,0)=0∂u∂t∣t=0=f(x)}0<x<L\left.\begin{array}{c}u(x, 0)=0 \\\left.\frac{\partial u}{\partial t}\right\vert_{t=0}=f(x)\end{array}\right\} 0<x<L
    Solution
    • (a) - (e) - (g)
    • (b) - (f) - (i)
    • (c) - (d) - (h)