Skip to main content

Tutorial 11: Fourier Series Expansion & Its Application

Tutorial Question

  1. The function f(t)=1−t2f(t)=1-t^{2} is to be represented by a Fourier series expansion over the finite interval 0<t<10<t<1. Obtain a suitable

    a. full-range series expansion

    b. half-range sine series expansion

    c. half-range cosine series expansion

    Solution

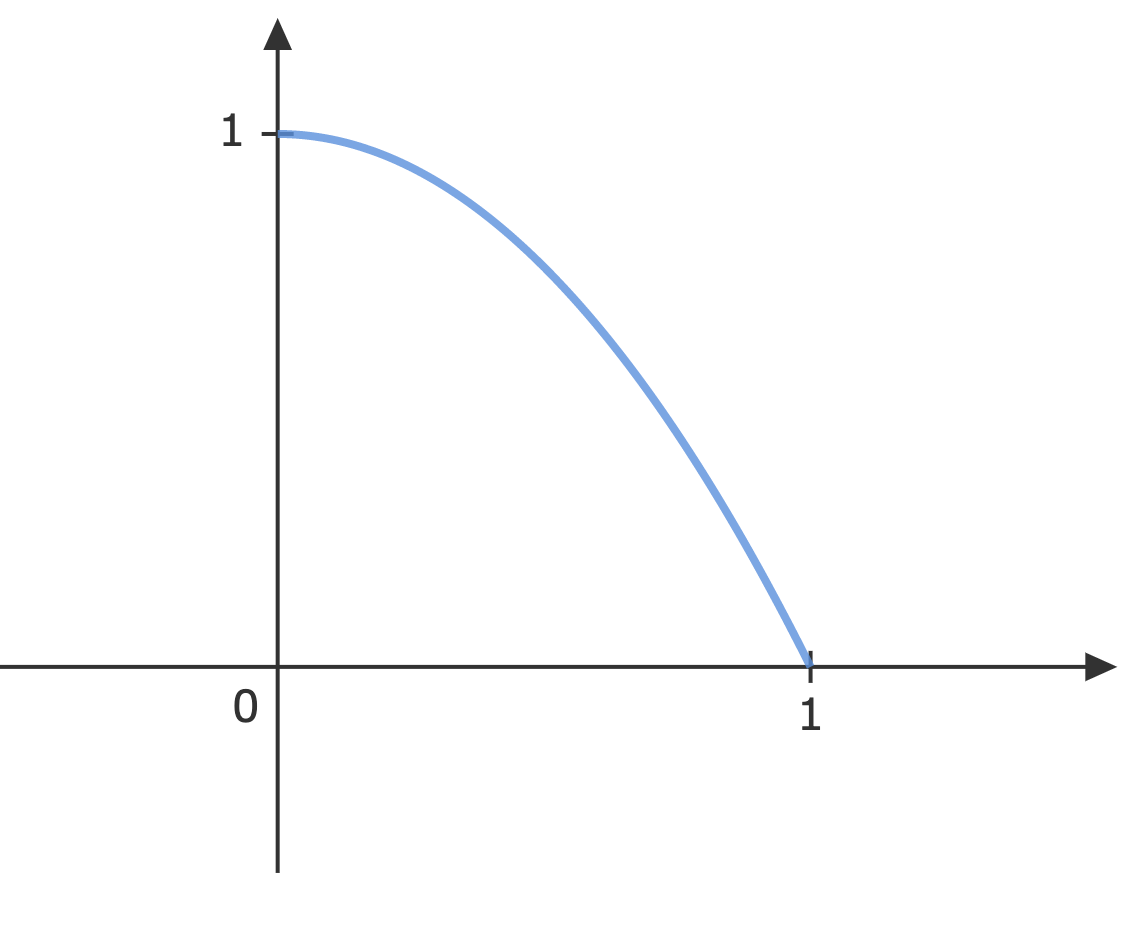
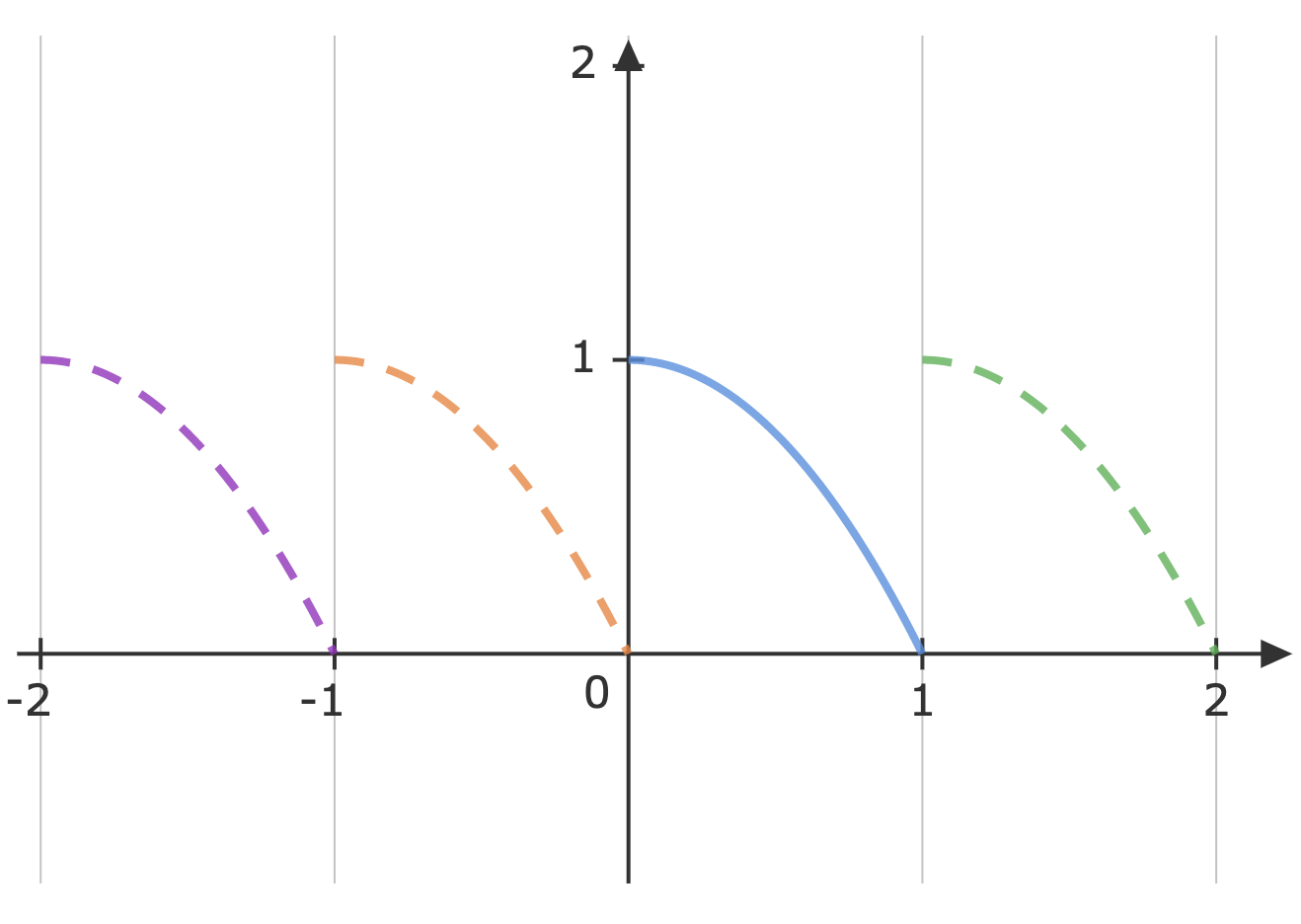
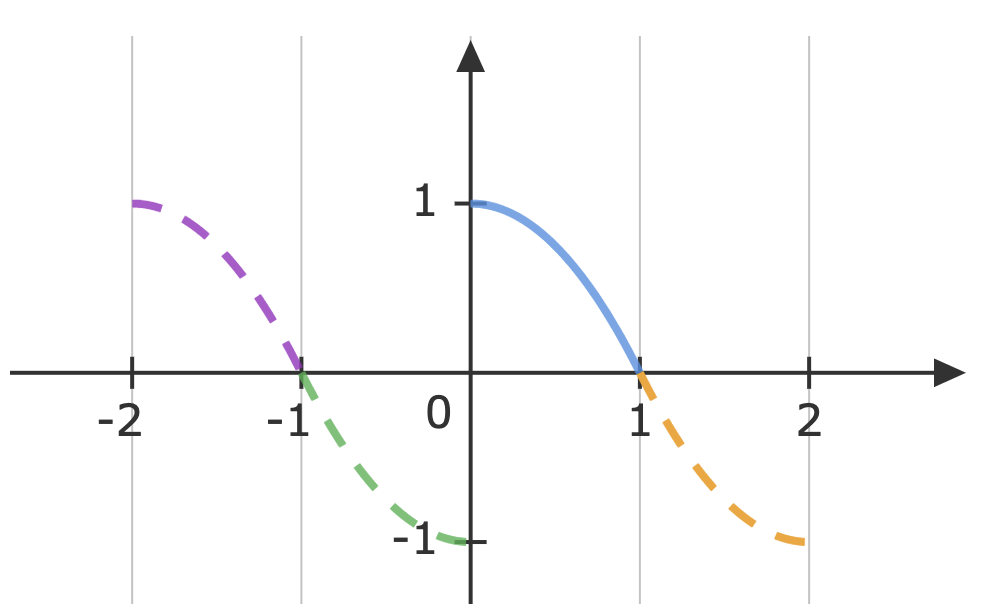
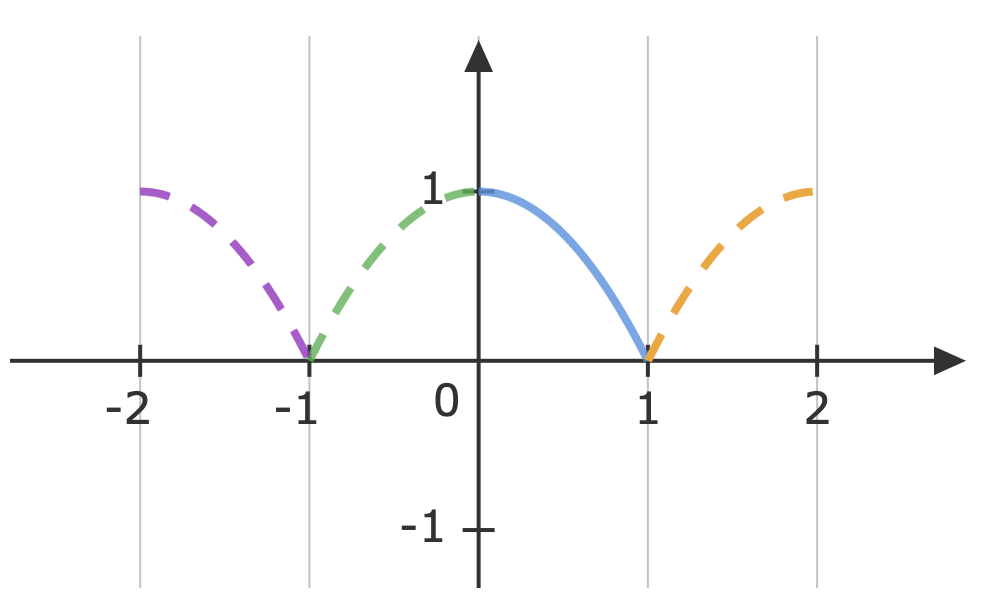
    a. For full-range series expansion, P=1,L=12P=1, L=\frac{1}{2}

    a0=∫011−t2dr=[t−t33]01=23an=2∫01(1−t2)cos⁡2nπtdt={[12nπsin⁡2nπt(1−t2)]01−∫0112nπsin⁡2nπt(−2t)dt}=2{0−12nπ[−12nπcos⁡2nπt(−2t)]01−(12nπ)×∫011nπcos⁡2nπtdt}=2{−2(2nπ)2cos⁡2nπ}=−1(nπ)2cos⁡2nπ=−1(nπ)2since cos⁡2nπ=1 for integers nbn=2∫01(1−t)2sin⁡2nπtdt=2{[−12nπcos⁡2nπt(1−t2)]01+12nπ∫01cos⁡2nπt(−2t)dt}=2{12nπcos⁡0−22nπ[[12nπsin⁡2nπt(t)]01−12nπ∫01sin⁡2nπtdt]}=2{12nπ−2(2nπ)3[cos⁡2nπt]01}=2{12nπ−2(2nπ)3cos⁡2nπ+2(2nπ)3cos⁡0}=1nπ∴f(t)=1−t2=23−1π2∑n=1∞1n2cos⁡2nπt+1π∑n=1∞1nsin⁡2nπt\begin{aligned}a_0&=\int_0^11-t^2dr\\&=\left[t-\frac{t^3}{3}\right]_0^1=\frac{2}{3}\\a_n&=2\int_0^1(1-t^2)\cos2n\pi tdt\\&=\left\{\left[\frac{1}{2n\pi}\sin 2n\pi t(1-t^2)\right]_0^1-\int_0^1\frac{1}{2n\pi}\sin2n\pi t(-2t)dt\right\}\\&=2\left\{0-\frac{1}{2n\pi}\left[-\frac{1}{2n\pi}\cos2n\pi t(-2t)\right]_0^1-\left(\frac{1}{2n\pi}\right)\times\int_0^1\frac{1}{n\pi}\cos2n\pi tdt\right\}\\&=2\left\{-\frac{2}{(2n\pi)^2}\cos2n\pi\right\}\\&=-\frac{1}{(n\pi)^2}\cos2n\pi\\&=-\frac{1}{(n\pi)^2}\quad\text{since }\cos2n\pi=1\text{ for integers }n\\\\b_n&=2\int_0^1(1-t)^2\sin2n\pi tdt\\&=2\left\{\left[-\frac{1}{2n\pi }\cos2n\pi t(1-t^2)\right]_0^1+\frac{1}{2n\pi}\int_0^1\cos2n\pi t(-2t)dt\right\}\\&=2\left\{\frac{1}{2n\pi}\cos0-\frac{2}{2n\pi}\left[\left[\frac{1}{2n\pi}\sin2n\pi t (t)\right]_0^1-\frac{1}{2n\pi}\int_0^1\sin2n\pi tdt\right]\right\}\\&=2\left\{\frac{1}{2n\pi}-\frac{2}{(2n\pi)^3}\left[\cos2n\pi t\right]_0^1\right\}\\&=2\left\{\frac{1}{2n\pi}-\frac{2}{(2n\pi)^3}\cos2n\pi+\frac{2}{(2n\pi)^3}\cos 0\right\}\\&=\frac{1}{n\pi}\\\\\therefore f(t)&=1-t^2=\frac{2}{3}-\frac{1}{\pi^2}\sum_{n=1}^\infty\frac{1}{n^2}\cos2n\pi t+\frac{1}{\pi}\sum_{n=1}^\infty\frac{1}{n}\sin2n\pi t\end{aligned}

    b. For half-range sine series, P=2,L=1P=2,L=1

    bn=2∫01(1−t2)sin⁡nπtdt=2{[−1nπcos⁡nπt(1−t2)]01+1nπ∫01cos⁡nπt(−2t)dr}=2{1nπcos⁡0−2nπ[[1nπsin⁡nπt(t)]01−1nπ∫01sin⁡nπtdt]}=2{1nπ+2(nπ)2×(−1nπ)[cos⁡nπt]01}=2{1nπ−2(nπ)3cos⁡nπ+2(nπ)3×1}\begin{aligned}b_n&=2\int_0^1(1-t^2)\sin n\pi tdt\\&=2\left\{\left[-\frac{1}{n\pi}\cos n\pi t(1-t^2)\right]_0^1+\frac{1}{n\pi}\int_0^1\cos n\pi t(-2t)dr\right\}\\&=2\left\{\frac{1}{n\pi}\cos0-\frac{2}{n\pi}\left[\left[\frac{1}{n\pi}\sin n\pi t(t)\right]_0^1-\frac{1}{n\pi}\int_0^1\sin n\pi tdt\right]\right\}\\&=2\left\{\frac{1}{n\pi}+\frac{2}{(n\pi)^2}\times\left(-\frac{1}{n\pi}\right)\left[\cos n\pi t\right]_0^1\right\}\\&=2\left\{\frac{1}{n\pi}-\frac{2}{(n\pi)^3}\cos n\pi+\frac{2}{(n\pi)^3}\times1\right\}\end{aligned}

    From cos⁡nπ=(−1)n={−1for odd n1for even n\cos n\pi=(-1)^n=\begin{cases}-1&\quad\text{for odd } n\\1&\quad\text{for even }n\end{cases}

    When nn is odd,

    bn=2[1nπ−2(nπ)3(−1)+2(nπ)3]=2(1nπ+4(nπ)3)\begin{aligned}b_n&=2\left[\frac{1}{n\pi}-\frac{2}{(n\pi)^3}(-1)+\frac{2}{(n\pi)^3}\right]\\&=2\left(\frac{1}{n\pi}+\frac{4}{(n\pi)^3}\right)\end{aligned}

    When nn is even,

    bn=2(1nπ−2(nπ)3+2(nπ)3)=2nπb_n=2\left(\frac{1}{n\pi}-\frac{2}{(n\pi)^3}+\frac{2}{(n\pi)^3}\right)=\frac{2}{n\pi}∴f(t)=2π∑n=1∞1nsin⁡2nπt+2π∑n=1∞(12n−1−4(2n−1)3π2)sin⁡(2n−1)πt\therefore f(t)=\frac{2}{\pi}\sum_{n=1}^\infty \frac{1}{n}\sin2n\pi t+\frac{2}{\pi}\sum_{n=1}^\infty\left(\frac{1}{2n-1}-\frac{4}{(2n-1)^3\pi^2}\right)\sin(2n-1)\pi t

    c. Half-range cosine:

    a0=∫01(1−t2)dt=23an=2∫01(1−t2)cos⁡nπtdt=2{[1nπsin⁡nπt(1−t2)]01−1nπ∫01sin⁡nπt(−2t)dt}=4nπ{[−tnπcos⁡nπt]01+1nπ∫01cos⁡nπtdt}=4nπ{−1nπcos⁡nπ+1(nπ)2[sin⁡nπt]01}=−4(nπ)2cos⁡nπ=−4(nπ)2(−1)n=4(nπ)2(−1)n+1\begin{aligned}a_0&=\int_0^1(1-t^2)dt=\frac{2}{3}\\a_n&=2\int_0^1(1-t^2)\cos n\pi tdt\\&=2\left\{\left[\frac{1}{n\pi}\sin n\pi t(1-t^2)\right]_0^1-\frac{1}{n\pi}\int_0^1\sin n\pi t(-2t)dt\right\}\\&=\frac{4}{n\pi}\left\{\left[-\frac{t}{n\pi}\cos n\pi t\right]_0^1+\frac{1}{n\pi}\int_0^1\cos n\pi tdt\right\}\\&=\frac{4}{n\pi}\left\{-\frac{1}{n\pi}\cos n\pi+\frac{1}{(n\pi)^2}\left[\sin n\pi t\right]_0^1\right\}\\&=-\frac{4}{(n\pi)^2}\cos n\pi\\&=-\frac{4}{(n\pi)^2}(-1)^n=\frac{4}{(n\pi)^2}(-1)^{n+1}\end{aligned}∴f(t)=1−t2=23+4π2∑n=1∞(−1)n+1n2cos⁡nπt\therefore f(t)=1-t^2=\frac{2}{3}+\frac{4}{\pi^2}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^2}\cos n\pi t

  2. Sketch the graphs of:

    a. full-range series expansion

    b. half-range sine series expansion

    c. half-range cosine series expansion

    for f(t)=1−t2f(t)=1-t^{2} in Q1 for −2<t<2-2<t<2. Draw and label the period pp and the finite interval τ\tau on each graph.

    Solution

    The original function:

    a.

    p=1,τ=1p=1,\tau=1

    b.

    p=2,τ=1p=2,\tau=1

    c.

    p=2,τ=1p=2,\tau=1

  3. The temperature distribution T(x)T(x) at a distance xx, measured from one end, along a bar of length 10 inch is given by:

    T(x)=2x(10−x)(0≤x≤10)T(x)=2 x(10-x) \quad(0 \leq x \leq 10)

    Express T(x)T(x) as a Fourier series expansion consisting of sine terms only.

    Solution
    T(x)=2x(10−x)T(x)=∑n=1∞bnsin⁡nπ10x\begin{aligned}T(x)&=2 x(10-x) \\T(x)&=\sum_{n=1}^\infty b_n\sin\frac{n\pi}{10}x\end{aligned}

    where

    bn=210∫0102x(10−x)sin⁡nπ10xdx=25∫010(10x−x2)sin⁡nπ10xdx\begin{aligned}b_n&=\frac{2}{10}\int_0^{10}2x(10-x)\sin\frac{n\pi}{10}xdx\\&=\frac{2}{5}\int_0^{10}(10x-x^2)\sin\frac{n\pi}{10}xdx\end{aligned}

    Consider

    ∫010(10xsin⁡nπ10x)dx=[10x(−10nπ)cos⁡nπ10x]010+∫010102nπcos⁡nπ10xdx=−103nπcos⁡nπ+0+[102nπ×10nπsin⁡nπ10x]010=−103nπcos⁡nπ\begin{aligned}&\int_0^{10}\left(10x\sin\frac{n\pi}{10}x\right)dx\\&=\left[10x\left(-\frac{10}{n\pi}\right)\cos\frac{n\pi}{10}x\right]_0^{10}+\int_0^{10}\frac{10^2}{n\pi}\cos\frac{n\pi}{10}xdx\\&=-\frac{10^3}{n\pi}\cos n\pi+0+\left[\frac{10^2}{n\pi}\times\frac{10}{n\pi}\sin\frac{n\pi}{10}x\right]_0^{10}\\&=-\frac{10^3}{n\pi}\cos n\pi\end{aligned}

    Consider

    ∫010x2sin⁡nπ10xdx=[x2(−10nπ)cos⁡nπ10x]010+∫01010nπ(2x)cos⁡nπ10xdx=(−103nπcos⁡nπ+0)+[20xnπ(10nπ)sin⁡nπ10x]010−∫010200n2π2sin⁡nπ10xdx=−103nπcos⁡nπ−[200n2π2(−10nπ)cos⁡nπ10x]010=−103nπcos⁡nπ−(−2×103n3π3cos⁡nπ+2×103n3π3)=−103nπcos⁡nπ+2×103n3π3(cos⁡nπ−1)\begin{aligned}&\int_0^{10}x^2\sin\frac{n\pi}{10}xdx\\&=\left[x^2\left(-\frac{10}{n\pi}\right)\cos\frac{n\pi}{10}x\right]_0^{10}+\int_0^{10}\frac{10}{n\pi}(2x)\cos\frac{n\pi}{10}xdx\\&=\left(-\frac{10^3}{n\pi}\cos n\pi+0\right)+\left[\frac{20x}{n\pi}\left(\frac{10}{n\pi}\right)\sin\frac{n\pi}{10}x\right]_0^{10}-\int_0^{10}\frac{200}{n^2\pi^2}\sin\frac{n\pi}{10}xdx\\&=-\frac{10^3}{n\pi}\cos n\pi-\left[\frac{200}{n^2\pi^2}\left(-\frac{10}{n\pi}\right)\cos \frac{n\pi}{10}x \right]_0^{10}\\&=-\frac{10^3}{n\pi}\cos n\pi-\left(-\frac{2\times10^3}{n^3\pi^3}\cos n\pi+\frac{2\times10^3}{n^3\pi^3}\right)\\&=-\frac{10^3}{n\pi}\cos n\pi+\frac{2\times10^3}{n^3\pi^3}(\cos n\pi-1)\end{aligned}bn=25{−103nπcos⁡nπ+103nπcos⁡nπ−2×103n3π3(cos⁡nπ−1)}=25×2×103n3π3(1−cos⁡nπ)=800n3π3(1−cos⁡nπ)\begin{aligned}b_n&=\frac{2}{5}\left\{-\frac{10^3}{n\pi}\cos n\pi+\frac{10^3}{n\pi}\cos n\pi-\frac{2\times10^3}{n^3\pi^3}(\cos n\pi-1)\right\}\\&=\frac{2}{5}\times\frac{2\times10^3}{n^3\pi^3}(1-\cos n\pi)\\&=\frac{800}{n^3\pi^3}(1-\cos n\pi)\end{aligned}

    Since cos⁡nπ={1for n is even−1for n is odd\cos n\pi=\begin{cases}1&\quad\text{for }n\text{ is even}\\-1&\quad\text{for }n\text{ is odd}\end{cases},

    bn={0for n is even1600n3π3for n is oddb_n=\begin{cases}0&\quad\text{for }n\text{ is even}\\\frac{1600}{n^3\pi^3}&\quad\text{for }n\text{ is odd}\end{cases}∴T(x)=∑n=1∞bnsin⁡nπLx=∑n=1∞1600π3(12n−1)3sin⁡(2n−1)π10xor=∑n=1,3,5,...∞1600π31n3sin⁡nπ10x\begin{aligned}\therefore T(x)&=\sum_{n=1}^\infty b_n\sin\frac{n\pi}{L}x\\&=\sum_{n=1}^\infty\frac{1600}{\pi^3}\left(\frac{1}{2n-1}\right)^3\sin\frac{(2n-1)\pi}{10}x\\\\\text{or}\\\\&=\sum_{n=1,3,5,...}^\infty \frac{1600}{\pi^3}\frac{1}{n^3}\sin\frac{n\pi}{10}x\end{aligned}

  4. Suppose a uniform beam of length LL is simply supported at x=0x=0 and at x=Lx=L. If the load per unit length is given by w(x)=w0xL,0<x<Lw(x)=\frac{w_{0} x}{L}, 0<x<L, then the differential equation for the deflection y(x)y(x) is

    EId4ydx4=w0xLE I \frac{d^{4} y}{d x^{4}}=\frac{w_{0} x}{L}

    where E,IE, I and w0w_{0} are constants.

    a. Expand w(x)w(x) in a half-range sine series.

    b. Find a particular solution y(x)y(x) of the differential equation.

    Solution

    a.

    bn=2L∫0Lw0xLsin⁡nπLxdx=2w0L2∫0Lxsin⁡nπLxdx=2w0L2{[−Lnπcos⁡nπLx(x)]0L+Lnπ∫0Lcos⁡nπLxdx}=2w0L2{−L2nπcos⁡nπ}=−2w0nπcos⁡nπ=2w0nπ(−1)n+1\begin{aligned}b_n&=\frac{2}{L}\int_0^L\frac{w_0x}{L}\sin\frac{n\pi}{L}xdx\\&=\frac{2w_0}{L^2}\int_0^Lx\sin\frac{n\pi}{L}xdx\\&=\frac{2w_0}{L^2}\left\{\left[-\frac{L}{n\pi}\cos\frac{n\pi}{L}x(x)\right]_0^L+\frac{L}{n\pi}\int_0^L\cos\frac{n\pi}{L}xdx\right\}\\&=\frac{2w_0}{L^2}\left\{-\frac{L^2}{n\pi}\cos n\pi\right\}\\&=-\frac{2w_0}{n\pi}\cos n\pi=\frac{2w_0}{n\pi}(-1)^{n+1}\end{aligned}

    b. From EId4ydx4=w0xLE I \frac{d^{4} y}{d x^{4}}=\frac{w_{0} x}{L},

    EId4ydx4=2w0nπ(−1)n+1sin⁡nπLxE I \frac{d^{4} y}{d x^{4}}=\frac{2w_{0}}{n\pi}(-1)^{n+1}\sin\frac{n\pi}{L}x

    Let

    EId4ydx4=2w0nπ(−1)n+1sin⁡nπLxE I \frac{d^{4} y}{d x^{4}}=\frac{2w_{0}}{n\pi}(-1)^{n+1}\sin\frac{n\pi}{L}x∴∑n=1∞EIn4π4L4βnsin⁡nπLx=∑n=1∞2w0nπ(−1)n+1sin⁡nπLxEIn4π4L4βn=2w0nπ(−1)n+1βn=2w0L4EIπ5n5(−1)n+1\begin{aligned}\therefore \sum_{n=1}^\infty EI\frac{n^4\pi^4}{L^4}\beta_n\sin\frac{n\pi}{L}x&=\sum_{n=1}^\infty\frac{2w_0}{n\pi}(-1)^{n+1}\sin\frac{n\pi}{L}x\\EI\frac{n^4\pi^4}{L^4}\beta_n&=\frac{2w_0}{n\pi}(-1)^{n+1}\\\beta_n&=\frac{2w_0L^4}{EI\pi^5n^5}(-1)^{n+1}\end{aligned}∴y(x)=2woL4EIπ5∑n=1∞(−1)n+1n5sin⁡nπLx\therefore y(x)=\frac{2w_oL^4}{EI\pi^5}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^5}\sin\frac{n\pi}{L}x