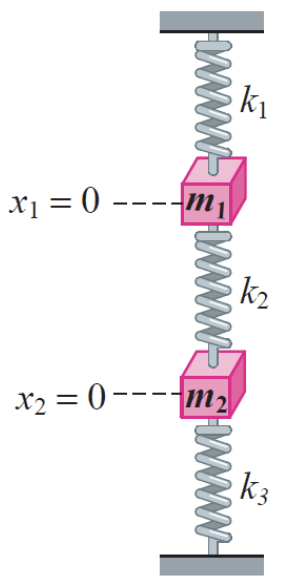Skip to main content

Tutorial 9: Laplace Transform 2

Tutorial Question

  1. Evaluate the given Laplace transform.

    i. L{tsinh⁡3t}\mathcal{L}\{t \sinh 3 t\}

    ii. L{te−3tcos⁡3t}\mathcal{L}\left\{t e^{-3 t} \cos 3 t\right\}

    iii. L{e2t∗sin⁡t}\mathcal{L}\left\{e^{2 t} * \sin t\right\}

    iv. L{e−t∗etcos⁡t}\mathcal{L}\left\{e^{-t} * e^{t} \cos t\right\}

    v. L{∫0tτsin⁡τdτ}\mathcal{L}\left\{\int_{0}^{t} \tau \sin \tau d \tau\right\}

    vi. L{t∫0tsin⁡τdτ}\mathcal{L}\left\{t \int_{0}^{t} \sin \tau d \tau\right\}

    Solution

    i.

    L{tsinh⁡3t}=−dds(3s2−32)=6s(s2−9)2\begin{aligned}\mathcal{L}\{t \sinh 3 t\}&=-\frac{d}{d s}\left(\frac{3}{s^{2}-3^{2}}\right)\\&=\frac{6 s}{\left(s^{2}-9\right)^{2}}\end{aligned}

    ii.

    L{te−3tcos⁡3t}=−dds(s+3(s+3)2+32)=−[(s+3)2+9](1)−(s+3)2(s+3)[(s+3)2+9]2=−(s+3)2+9−2(s+3)2[(s+3)2+9]2=(s+3)2−9[(s+3)2+9]2\begin{aligned} \mathcal{L}\left\{t e^{-3 t} \cos 3 t\right\} &=-\frac{d}{d s}\left(\frac{s+3}{(s+3)^{2}+3^{2}}\right) \\ &=-\frac{\left[(s+3)^{2}+9\right](1)-(s+3) 2(s+3)}{\left[(s+3)^{2}+9\right]^{2}} \\ &=-\frac{(s+3)^{2}+9-2(s+3)^{2}}{\left[(s+3)^{2}+9\right]^{2}} \\ &=\frac{(s+3)^{2}-9}{\left[(s+3)^{2}+9\right]^{2}} \end{aligned}

    iii.

    L{e2t∗sin⁡t}=1(s−2)(s2+1)\mathcal{L}\left\{e^{2 t} * \sin t\right\}=\frac{1}{(s-2)\left(s^{2}+1\right)}

    iv.

    L{e−t∗etcos⁡t}=s−1(s+1)[(s−1)2+1]\mathcal{L}\left\{e^{-t} * e^{t} \cos t\right\}=\frac{s-1}{(s+1)\left[(s-1)^{2}+1\right]}

    v.

    L{∫0tτsin⁡τdτ}=1sL{tsin⁡t}=1s(−dds(1s2+1))=−1s(−2s(s2+1)2)=2(s2+1)2\begin{aligned} \mathcal{L}\left\{\int_{0}^{t} \tau \sin \tau d \tau\right\} &=\frac{1}{s} \mathcal{L}\{t \sin t\}=\frac{1}{s}\left(-\frac{d}{d s}\left(\frac{1}{s^{2}+1}\right)\right) \\ &=-\frac{1}{s}\left(-\frac{2 s}{\left(s^{2}+1\right)^{2}}\right) \\ &=\frac{2}{\left(s^{2}+1\right)^{2}} \end{aligned}

    vi.

    L{t∫0tsin⁡τdτ}=−dds(L{∫0tsin⁡τdτ})=−dds(1s1s2+1)=−(1s(−2s(s2+1)2)−1s2(1s2+1))=3s2+1s2(s2+1)2\begin{aligned} \mathcal{L}\left\{t \int_{0}^{t} \sin \tau d \tau\right\} &=-\frac{d}{d s}\left(\mathcal{L}\left\{\int_{0}^{t} \sin \tau d \tau\right\}\right) \\ &=-\frac{d}{d s}\left(\frac{1}{s} \frac{1}{s^{2}+1}\right) \\ &=-\left(\frac{1}{s}\left(-\frac{2 s}{\left(s^{2}+1\right)^{2}}\right)-\frac{1}{s^{2}}\left(\frac{1}{s^{2}+1}\right)\right) \\ &=\frac{3 s^{2}+1}{s^{2}\left(s^{2}+1\right)^{2}} \end{aligned}

  2. Use the Laplace transform to solve the initial-value problem.

    i. dydt+3y=13sin⁡2t,y(0)=6\frac{d y}{d t}+3 y=13 \sin 2 t, y(0)=6

    ii. y′′+16y=f(t),y(0)=0,y′(0)=1y^{\prime \prime}+16 y=f(t), y(0)=0, y^{\prime}(0)=1 where f(t)={cos⁡4t,0≤t≤π0,t≥πf(t)=\left\{\begin{array}{cc}\cos 4 t, & 0 \leq t \leq \pi \\ 0, & t \geq \pi\end{array}\right.

    iii. y′+y=δ(t−1),y(0)=2y^{\prime}+y=\delta(t-1), y(0)=2

    iv. y′′−7y′+6y=et+δ(t−2)+δ(t−4),y(0)=0,y′(0)=0y^{\prime \prime}-7 y^{\prime}+6 y=e^{t}+\delta(t-2)+\delta(t-4), \quad y(0)=0, y^{\prime}(0)=0

    v. y′′+y=δ(t−12π)+δ(t−32π),y(0)=0,y′(0)=0y^{\prime \prime}+y=\delta\left(t-\frac{1}{2} \pi\right)+\delta\left(t-\frac{3}{2} \pi\right), \quad y(0)=0, \quad y^{\prime}(0)=0

    Solution

    i.

    L(dydt)+3L(y)=13L(sin⁡2t)sY(s)−y(0)+3Y(s)=132s2+4(s+3)Y(s)=6+26s2+4Y(s)=6s+3+26(s+3)(s2+4)Y(s)=6s2+50(s+3)(s2+4)\begin{aligned} \mathcal{L}\left(\frac{d y}{d t}\right)+3 \mathcal{L}(y)&=13 \mathcal{L}(\sin 2 t) \\ s Y(s)-y(0)+3 Y(s)&=13 \frac{2}{s^{2}+4} \\ (s+3) Y(s)&=6+\frac{26}{s^{2}+4}\\Y(s)&=\frac{6}{s+3}+\frac{26}{(s+3)\left(s^{2}+4\right)}\\Y(s)&=\frac{6 s^{2}+50}{(s+3)\left(s^{2}+4\right)} \end{aligned}

    Let 6s2+50(s+3)(s2+4)=As+3+Bs+Cs2+4⇒A=8,B=−2,C=6\frac{6 s^{2}+50}{(s+3)\left(s^{2}+4\right)}=\frac{A}{s+3}+\frac{B s+C}{s^{2}+4} \quad \Rightarrow \quad A=8, \quad B=-2, \quad C=6

    Y(s)=6s2+50(s+3)(s2+4)=8s+3+6−2ss2+4\begin{aligned}Y(s)&=\frac{6 s^{2}+50}{(s+3)\left(s^{2}+4\right)}=\frac{8}{s+3}+\frac{6-2 s}{s^{2}+4} \\ \end{aligned}∴y(t)=L−1(8s+3+6−2ss2+4)=8e−3t+3sin⁡2t−2cos⁡2t\therefore y(t)=\mathcal{L}^{-1}\left(\frac{8}{s+3}+\frac{6-2 s}{s^{2}+4}\right)=8 e^{-3 t}+3 \sin 2 t-2 \cos 2 t

    ii. The Laplace transform of the differential equation is

    s2L{y}−sy(0)−y′(0)+16L{y}=L{cos⁡4tu(t)−cos⁡4tu(t−π)}s2L{y}−s(0)−1+16L{y}=ss2+16−se−πss2+16(s2+16)L{y}=1+ss2+16−se−πss2+16L{y}=1s2+16+s(s2+16)2−se−πs(s2+16)2\begin{aligned} s^{2} \mathcal{L}\{y\}-s y(0)-y^{\prime}(0)+16 \mathcal{L}\{y\}&=\mathcal{L}\{\cos 4 t u(t)-\cos 4 t u(t-\pi)\}\\s^{2} \mathcal{L}\{y\}-s(0)-1+16 \mathcal{L}\{y\}&=\frac{s}{s^{2}+16}-\frac{s e^{-\pi s}}{s^{2}+16}\\\left(s^{2}+16\right) \mathcal{L}\{y\}&=1+\frac{s}{s^{2}+16}-\frac{s e^{-\pi s}}{s^{2}+16}\\\mathcal{L}\{y\}&=\frac{1}{s^{2}+16}+\frac{s}{\left(s^{2}+16\right)^{2}}-\frac{s e^{-\pi s}}{\left(s^{2}+16\right)^{2}} \end{aligned}y(t)=14sin⁡4t+18tsin⁡4t−18(t−π)sin⁡4(t−π)u(t−π)y(t)=\frac{1}{4} \sin 4 t+\frac{1}{8} t \sin 4 t-\frac{1}{8}(t-\pi) \sin 4(t-\pi) u(t-\pi)

    iii. The Laplace transform of the differential equation is

    sY(s)−y′(0)+Y(s)=e−s(s+1)Y(s)=2+e−sY(s)=2s+1+e−ss+1\begin{aligned} s Y(s)-y^{\prime}(0)+Y(s)&=e^{-s} \\ (s+1) Y(s)&=2+e^{-s} \\ Y(s)&=\frac{2}{s+1}+\frac{e^{-s}}{s+1} \\ \end{aligned}y(t)=2e−t+e−(t−1)u(t−1)y(t)=2 e^{-t}+e^{-(t-1)} u(t-1)

    iv. The Laplace transform of the differential equation is

    s2Y(s)−sy(0)−y′(0)−7(sY(s)−y(0))+6Y(s)=1s−1+e−2s+e−4s(s2−7s+6)Y(s)=1s−1+e−2s+e−4s\begin{aligned} s^{2} Y(s)-s y(0)-y^{\prime}(0)-7(s Y(s)-y(0))+6 Y(s)&=\frac{1}{s-1}+e^{-2 s}+e^{-4 s} \\ \left(s^{2}-7 s+6\right) Y(s)&=\frac{1}{s-1}+e^{-2 s}+e^{-4 s} \\ \end{aligned}Y(s)=1(s−1)2(s−6)+e−2s(s−1)(s−6)+e−4s(s−1)(s−6)Y(s)=\frac{1}{(s-1)^{2}(s-6)}+\frac{e^{-2 s}}{(s-1)(s-6)}+\frac{e^{-4 s}}{(s-1)(s-6)}

    Let 1(s−1)(s−6)=As−1+Bs−6⇒A=−15,B=15\frac{1}{(s-1)(s-6)}=\frac{A}{s-1}+\frac{B}{s-6} \Rightarrow \quad A=-\frac{1}{5}, B=\frac{1}{5}

    Let 1(s−1)2(s−6)=Cs−1+D(s−1)2+Es−6⇒C=−125,D=−15,E=125\frac{1}{(s-1)^{2}(s-6)}=\frac{C}{s-1}+\frac{D}{(s-1)^{2}}+\frac{E}{s-6} \quad \Rightarrow \quad C=-\frac{1}{25}, \quad D=-\frac{1}{5}, \quad E=\frac{1}{25}

    Y(s)=−1251s−1−151(s−1)2+1251s−6+(−151s−1+151s−6)(e−2s+e−4s)Y(s)=-\frac{1}{25} \frac{1}{s-1}-\frac{1}{5} \frac{1}{(s-1)^{2}}+\frac{1}{25} \frac{1}{s-6}+\left(-\frac{1}{5} \frac{1}{s-1}+\frac{1}{5} \frac{1}{s-6}\right)\left(e^{-2 s}+e^{-4 s}\right)f(t)=−125et−15tet+125e6t+(−15e(t−2)+15e6(t−2))u(t−2)+(−15e(t−4)+15e6(t−4))u(t−4)\begin{aligned}f(t)&=-\frac{1}{25} e^{t}-\frac{1}{5} t e^{t}+\frac{1}{25} e^{6 t}+\left(-\frac{1}{5} e^{(t-2)}+\frac{1}{5} e^{6(t-2)}\right) u(t-2)\\&\quad+\left(-\frac{1}{5} e^{(t-4)}+\right. \left.\frac{1}{5} e^{6(t-4)}\right) u(t-4)\end{aligned}

    v.

    s2Y(s)−sy(0)−y′(0)+Y(s)=e−π2s+e−3π2s(s2+1)Y(s)=e−π2s+e−3π2sY(s)=e−π2ss2+1+e−3π2ss2+1\begin{aligned} s^{2} Y(s)-s y(0)-y^{\prime}(0)+Y(s)&=e^{-\frac{\pi}{2} s}+e^{-\frac{3 \pi}{2} s} \\ \left(s^{2}+1\right) Y(s)&=e^{-\frac{\pi}{2} s}+e^{-\frac{3 \pi}{2} s} \\ Y(s)&=\frac{e^{-\frac{\pi}{2} s}}{s^{2}+1}+\frac{e^{-\frac{3 \pi}{2} s}}{s^{2}+1} \\ \end{aligned}y(t)=sin⁡(t−π2)u(t−π2)+sin⁡(t−3π2)u(t−3π2)y(t)=−cos⁡tu(t−π2)+cos⁡tu(t−3π2)\begin{aligned}y(t)&=\sin \left(t-\frac{\pi}{2}\right) u\left(t-\frac{\pi}{2}\right)+\sin \left(t-\frac{3 \pi}{2}\right) u\left(t-\frac{3 \pi}{2}\right) \\ y(t)&=-\cos t u\left(t-\frac{\pi}{2}\right)+\cos t u\left(t-\frac{3 \pi}{2}\right)\end{aligned}

  3. Use the Laplace transform to solve the given system of differential equations.

    i. dxdt=−x+y,dydt=2x\frac{d x}{d t}=-x+y, \frac{d y}{d t}=2 x

    x(0)=0,y(0)=1\quad x(0)=0, y(0)=1

    ii. dxdt+3x+dydt=1,dxdt−x+dydt−y=et\frac{d x}{d t}+3 x+\frac{d y}{d t}=1, \frac{d x}{d t}-x+\frac{d y}{d t}-y=e^{t}

    x(0)=0,y(0)=0\quad x(0)=0, y(0)=0

    iii. dxdt−4x+d3ydt3=6sin⁡t,dxdt+2x−2d3ydt3=0\frac{d x}{d t}-4 x+\frac{d^{3} y}{d t^{3}}=6 \sin t, \frac{d x}{d t}+2 x-2 \frac{d^{3} y}{d t^{3}}=0

    x(0)=0,y(0)=0\quad x(0)=0, y(0)=0

    y′(0)=0,y′′(0)=0\quad y^{\prime}(0)=0, y^{\prime \prime}(0)=0

    Solution

    i.

    dxdt=−x+ysX−x(0)=−X+Y(s+1)X−Y=0(1)\begin{aligned} \frac{d x}{d t}=-x+y \\s X-x(0)=-X+Y \\(s+1) X-Y=0 \tag{1} \end{aligned}dydt=2xsY−y(0)=2X2X−sY=1(2)\begin{aligned} \frac{d y}{d t}=2 x \\s Y-y(0)=2 X \\2 X-s Y=1\tag{2} \end{aligned}

    From (1)(1), Y=(s+1)XY=(s+1) X and subsitute into (2)(2),

    2X−s[(s+1)X]=1X(2−s2+s)=1X=1(s−1)(s+2)Y=s+1(s−1)(s+2)\begin{aligned}2 X-s[(s+1) X]&=1\\X\left(2-s^{2}+s\right)&=1 \\X&=\frac{1}{(s-1)(s+2)} \\Y&=\frac{s+1}{(s-1)(s+2)}\end{aligned}

    By partial fraction,

    X=131s−1−131s+2Y=231s−1+131s+2\begin{aligned} X=\frac{1}{3} \frac{1}{s-1}-\frac{1}{3} \frac{1}{s+2} \\ Y=\frac{2}{3} \frac{1}{s-1}+\frac{1}{3} \frac{1}{s+2} \end{aligned}

    Therefore,

    x=13et−13e−2t;y=23et+13e−2tx=\frac{1}{3} e^{t}-\frac{1}{3} e^{-2 t} \quad ;\quad y=\frac{2}{3}e^t+\frac{1}{3}e^{-2t}

    ii.

    dxdt+3x+dydt=1sX−x(0)+3X+sY−y(0)=1s(s+3)X+sY=1s(1)\begin{aligned} \frac{d x}{d t}+3 x+\frac{d y}{d t}&=1\\s X-x(0)+3 X+s Y-y(0)&=\frac{1}{s}\\(s+3) X+s Y&=\frac{1}{s}\tag{1} \end{aligned}dxdt−x+dydt−y=etsX−x(0)−X+sY−y(0)−Y=1s−1(s−1)X+(s−1)Y=1s−1(2)\begin{aligned} \frac{d x}{d t}-x+\frac{d y}{d t}-y&=e^{t}\\s X-x(0)-X+s Y-y(0)-Y&=\frac{1}{s-1}\\(s-1) X+(s-1) Y&=\frac{1}{s-1}\tag{2} \end{aligned}[s+3ss−1s−1][XY]=[1/s1/(s−1)]\begin{aligned} {\left[\begin{array}{lc}s+3 & s \\ s-1 & s-1\end{array}\right]\left[\begin{array}{l}X \\ Y\end{array}\right]=\left[\begin{array}{c}1 / s \\ 1 /(s-1)\end{array}\right] } \end{aligned}

    Let A=[s+3ss−1s−1],X=[XY],B=[1/s1/(s−1)]A=\left[\begin{array}{cc}s+3 & s \\s-1 & s-1\end{array}\right], X=\left[\begin{array}{l}X \\Y\end{array}\right], B=\left[\begin{array}{c}1 / s \\1 /(s-1)\end{array}\right],

    X=A−1B=1(s+3)(s−1)−s(s−1)[s−1−s1−ss+3][1/s1/(s−1)][XY]=1s2+2s−3−s2+s[s−1s−ss−11−ss+s+3s−1][XY]=13(s−1)[(s−1)2−s2s(s−1)−(s−1)2+s2+3ss(s−1)][XY]=13s(s−1)2[−2s+15s−1]X=1−2s3s(s−1)2Y=5s−13s(s−1)2\begin{aligned} X&=A^{-1} B=\frac{1}{(s+3)(s-1)-s(s-1)}\left[\begin{array}{cc}s-1 & -s \\1-s & s+3\end{array}\right]\left[\begin{array}{c}1 / s \\1 /(s-1)\end{array}\right] \\ \left[\begin{array}{l}X \\Y\end{array}\right]&=\frac{1}{s^{2}+2 s-3-s^{2}+s}\left[\begin{array}{l}\frac{s-1}{s}-\frac{s}{s-1} \\\frac{1-s}{s}+\frac{s+3}{s-1}\end{array}\right] \\ \left[\begin{array}{l}X \\Y\end{array}\right]&=\frac{1}{3(s-1)}\left[\begin{array}{c}\frac{(s-1)^{2}-s^{2}}{s(s-1)} \\\frac{-(s-1)^{2}+s^{2}+3 s}{s(s-1)}\end{array}\right] \\ \left[\begin{array}{l}X \\Y\end{array}\right]&=\frac{1}{3 s(s-1)^{2}}\left[\begin{array}{c}-2 s+1 \\5 s-1\end{array}\right] \\ X&=\frac{1-2 s}{3 s(s-1)^{2}} \\ Y&=\frac{5 s-1}{3 s(s-1)^{2}}\end{aligned}

    By partial fraction,

    X=131s−131s−1−131(s−1)2Y=−131s+131s−1+431(s−1)2\begin{aligned} X=\frac{1}{3} \frac{1}{s}-\frac{1}{3} \frac{1}{s-1}-\frac{1}{3} \frac{1}{(s-1)^{2}}\\Y=-\frac{1}{3} \frac{1}{s}+\frac{1}{3} \frac{1}{s-1}+\frac{4}{3} \frac{1}{(s-1)^{2}} \end{aligned}

    Therefore,

    x=13−13et−13tet;y=−13+13et+43tetx=\frac{1}{3}-\frac{1}{3} e^{t}-\frac{1}{3} t e^{t} \quad ; \quad y=-\frac{1}{3}+\frac{1}{3} e^{t}+\frac{4}{3} t e^{t}

    iii.

    dxdt−4x+d3ydt3=6sin⁡tsL{x}−x(0)−4L{x}+s3L{y}−s2y′′(0)−sy′(0)−y(0)=6s2+1(s−4)L{x}+s3L{y}=6s2+1(1)\begin{aligned} \frac{d x}{d t}-4 x+\frac{d^{3} y}{d t^{3}}&=6 \sin t\\ s \mathcal{L}\{x\}-x(0)-4 \mathcal{L}\{x\}+s^{3} \mathcal{L}\{y\}-s^{2} y^{\prime \prime}(0)-s y^{\prime}(0)-y(0)&=\frac{6}{s^{2}+1} \\ (s-4) \mathcal{L}\{x\}+s^{3} \mathcal{L}\{y\}&=\frac{6}{s^{2}+1} \tag{1} \end{aligned}dxdt+2x−2d3ydt3=0sL{x}−x(0)+2L{x}−2(s3L{y}−s2y′′(0)−sy′(0)−y(0))=0(s+2)L{x}−2s3L{y}=0(2)\begin{aligned} \frac{d x}{d t}+2 x-2 \frac{d^{3} y}{d t^{3}}&=0 \\ s \mathcal{L}\{x\}-x(0)+2 \mathcal{L}\{x\}-2\left(s^{3} \mathcal{L}\{y\}-s^{2} y^{\prime \prime}(0)-s y^{\prime}(0)-y(0)\right)&=0 \\ (s+2) \mathcal{L}\{x\}-2 s^{3} \mathcal{L}\{y\}&=0\tag{2} \end{aligned}[s−4s3s+2−2s3][L{x}L{y}]=[6/(s2+1)0][L{x}L{y}]=1−2s4+8s3−s4−2s3[−2s3−s3−s−2s−4][6/(s2+1)0]L{x}=4(s−2)(s2+1)=451s−2−45ss2+1−851s2+1\begin{aligned}& \left[\begin{array}{cc}s-4 & s^{3} \\s+2 & -2 s^{3}\end{array}\right]\left[\begin{array}{c}\mathcal{L}\{x\} \\\mathcal{L}\{y\}\end{array}\right]=\left[\begin{array}{c}6 /\left(s^{2}+1\right) \\0\end{array}\right] \\ & \left[\begin{array}{l}\mathcal{L}\{x\} \\\mathcal{L}\{y\}\end{array}\right]=\frac{1}{-2 s^{4}+8 s^{3}-s^{4}-2 s^{3}}\left[\begin{array}{cc}-2 s^{3} & -s^{3} \\-s-2 & s-4\end{array}\right]\left[\begin{array}{c}6 /\left(s^{2}+1\right) \\0\end{array}\right] \\ & \mathcal{L}\{x\}=\frac{4}{(s-2)\left(s^{2}+1\right)}=\frac{4}{5} \frac{1}{s-2}-\frac{4}{5} \frac{s}{s^{2}+1}-\frac{8}{5} \frac{1}{s^{2}+1} \end{aligned}

    Then,

    x=45e2t−45cos⁡t−85sin⁡tx=\frac{4}{5} e^{2 t}-\frac{4}{5} \cos t-\frac{8}{5} \sin ty=1−2t−t2+15e2t−65cos⁡t+85sin⁡ty=1-2 t-t^{2}+\frac{1}{5} e^{2 t}-\frac{6}{5} \cos t+\frac{8}{5} \sin t

  4. Two masses m1m_{1} and m2m_{2} are connected to three springs of negligible mass having spring constants k1,k2k_{1}, k_{2} and k3k_{3}, respectively.

    Let x1x_{1} and x2x_{2} represent displacements of masses m1m_{1} and m2m_{2} from their equilibrium positions. The motion of the coupled system is represented by the system of second-order differential equations:

    m1d2x1dt2=−k1x1+k2(x2−x1)m2d2x2dt2=−k2(x2−x1)−k3x2\begin{aligned} &m_{1} \frac{d^{2} x_{1}}{d t^{2}}=-k_{1} x_{1}+k_{2}\left(x_{2}-x_{1}\right) \\ &m_{2} \frac{d^{2} x_{2}}{d t^{2}}=-k_{2}\left(x_{2}-x_{1}\right)-k_{3} x_{2} \end{aligned}

    Using Laplace transform to solve the system when k1=1,k2=1,k3=1,m1=1,m2=1k_{1}=1, k_{2}=1, k_{3}=1, m_{1}=1, m_{2}=1 and x1(0)=0,x1′(0)=−1,x2(0)=0,x2′(0)=1x_{1}(0)=0, x_{1}^{\prime}(0)=-1, x_{2}(0)=0, x_{2}^{\prime}(0)=1.

    Solution

    For m1d2x1dt2=−k1x1+k2(x2−x1)m_{1} \frac{d^{2} x_{1}}{d t^{2}}=-k_{1} x_{1}+k_{2}\left(x_{2}-x_{1}\right),

    Substitute unknowns:

    d2x1dt2=−x1+(x2−x1)=−2x1+x2\frac{d^{2} x_{1}}{d t^{2}}=-x_{1}+\left(x_{2}-x_{1}\right)=-2 x_{1}+x_{2}

    Laplace transform:

    s2X1(s)−sx1(0)−x1′(0)=−2X1(s)+X2(s)(1)s^{2} X_{1}(s)-s x_{1}(0)-x_{1}^{\prime}(0)=-2 X_{1}(s)+X_{2}(s) \tag{1}

    For m2d2x2dt2=−k2(x2−x1)−k3x2m_{2} \frac{d^{2} x_{2}}{d t^{2}}=-k_{2}\left(x_{2}-x_{1}\right)-k_{3} x_{2},

    Substitute unknowns:

    d2x2dt2=−(x2−x1)−x2=x1−2x2\frac{d^{2} x_{2}}{d t^{2}}=-\left(x_{2}-x_{1}\right)-x_{2}=x_{1}-2 x_{2}

    Laplace transform:

    s2X2(s)−sx2(0)−x2′(0)=X1(s)−2X2(s)(2)s^{2} X_{2}(s)-s x_{2}(0)-x_{2}^{\prime}(0)=X_{1}(s)-2 X_{2}(s)\tag{2}

    Hence,

    −X1(s)+(s2+2)X2(s)=1(3)-X_{1}(s)+\left(s^{2}+2\right) X_{2}(s)=1 \tag{3}

    From (1)(1),

    X2(s)=(s2+2)X1(s)+1(4)X_{2}(s)=\left(s^{2}+2\right) X_{1}(s)+1\tag{4}

    Substitute (4)(4) into (3)(3),

    −X1(s)+(s2+2)[(s2+2)X1(s)+1]=1(−1+s4+4s2+4)X1(s)+s2+2=1X1(s)=−s2+1(s2+1)(s2+3)=−1s2+3\begin{aligned}-X_{1}(s)+\left(s^{2}+2\right)\left[\left(s^{2}+2\right) X_{1}(s)+1\right]&=1\\\left(-1+s^{4}+4 s^{2}+4\right) X_{1}(s)+s^{2}+2&=1 \\ X_{1}(s)=-\frac{s^{2}+1}{\left(s^{2}+1\right)\left(s^{2}+3\right)}&=-\frac{1}{s^{2}+3}\end{aligned}

    Substitute X1(s)X_{1}(s) into (4)(4),

    X2(s)=(s2+2)[−1s2+3]+1X2(s)=−s2−2+s2+3s2+3=1s2+3\begin{aligned}X_{2}(s)&=\left(s^{2}+2\right)\left[-\frac{1}{s^{2}+3}\right]+1\\X_{2}(s)&=\frac{-s^{2}-2+s^{2}+3}{s^{2}+3}=\frac{1}{s^{2}+3}\end{aligned}

    Inverse Laplace,

    x1(t)=−13sin⁡3t;x2(t)=13sin⁡3tx_{1}(t)=-\frac{1}{\sqrt{3}} \sin \sqrt{3} t;\quad x_{2}(t)=\frac{1}{\sqrt{3}} \sin \sqrt{3} t

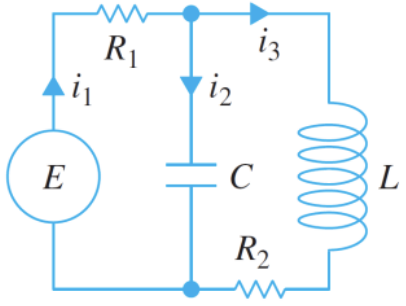
  5. The system of differential equations for the charge on the capacitor q(t)q(t) and the current i3(t)i_{3}(t) in the electrical network shown below is

    Find the charge on the capacitor q(t)q(t) using Laplace transform when L=1H,R1=1Ω,R2=1Ω,C=1F,E(t)={0,0<t<150e−t,t≥1,i3(0)=0,q(0)=0L=1 H, R_{1}=1 \Omega, R_{2}=1 \Omega, C=1 F, E(t)=\left\{\begin{array}{l}0,0<t<1 \\ 50 e^{-t}, t \geq 1\end{array}, i_{3}(0)=0, q(0)=0 \right..

    Solution
    dqdt+q+i3=50e−tu(t−1)dqdt+q+i3=50e−(t−1)−1u(t−1)\begin{aligned}\frac{d q}{d t}+q+i_{3}&=50 e^{-t} u(t-1)\\\frac{d q}{d t}+q+i_{3}&=50 e^{-(t-1)-1} u(t-1)\end{aligned}sQ(s)−q(0)+Q(s)+I3(s)=50e−1s+1e−s(s+1)Q(s)+I3(s)=50e−1s+1e−s(1)\begin{aligned} s Q(s)-q(0)+Q(s)+I_{3}(s)=\frac{50 e^{-1}}{s+1} e^{-s}\\ (s+1) Q(s)+I_{3}(s)=\frac{50 e^{-1}}{s+1} e^{-s}\tag{1} \end{aligned}di3dt+i3−q=0sI3(s)−i3(0)+I3(s)−Q(s)=0−Q(s)+(s+1)I3(s)=0(2)\begin{aligned} \frac{d i_{3}}{d t}+i_{3}-q=0\\ s I_{3}(s)-i_{3}(0)+I_{3}(s)-Q(s)=0\\ -Q(s)+(s+1) I_{3}(s)=0\tag{2} \end{aligned}

    Solving (1)(1) and (2)(2):

    Q(s)=50e−(s+1)(s+1)2+1q(t)=50e−1e−(t−1)sin⁡(t−1)u(t−1)=50e−tsin⁡(t−1)u(t−1)\begin{aligned} Q(s)&=\frac{50 e^{-(s+1)}}{(s+1)^{2}+1}\\q(t)&=50 e^{-1} e^{-(t-1)} \sin (t-1) u(t-1)\\ &=50 e^{-t} \sin (t-1) u(t-1) \end{aligned}