Tutorial 5: Engineering Applications of Differential Equations

Tutorial Question

1. a. Given the population of rabbit in human habitat (rabbit farm) grows at a rate proportional to the number of rabbit at time $t$ (year). It is observed that 200 and 800 rabbits are presented at 3rd year and 6th year respectively. What was the initial number of the rabbit, $y(0)=y_0$? How long does it take the population to double to $2y_0$.

   Solution

   Let $y=$ amount of rabit $\frac{d y(t)}{d t} \propto \mathrm{y}$. Hence, $\frac{d y(t)}{d t}=\mathrm{ky}$ where $\mathrm{k}$ is a constant.

   $\int \frac{d y(t)}{d t} d t=\int \mathrm{ky} d t \gg y(t)=\int \mathrm{ky} d t \quad$ [Complicated and cannot be solved]

   Use separable method,

   $$\begin{aligned} \frac{d y(t)}{\mathrm{y}}&=\mathrm{k} d t \\ \frac{d y(t)}{\mathrm{y}}&=\int \mathrm{k} d t \\ \ln y&=k t+C \gg>y=e^{k t+c} y&=\mathrm{A} e^{k t} \text{ where } \mathrm{A}=e^c \end{aligned}$$

   Given $y(3)=200 ; y(6)=800$, we get

   $$200=\mathrm{A} e^{3 k} \tag{1}$$

   and

   $$800=\mathrm{A} e^{6 k} \tag{2}$$

   Eqn (2) divided (1)

   $$\begin{aligned} \frac{800}{200}&=\frac{\mathrm{A} e^{6 k}}{\mathrm{~A} e^{3 k}} \\ 4&=e^{3 k} \\ k&=\frac{\ln 4}{3}=0.462 \\ 200&=\mathrm{A} e^{3(0.462)} \\ \mathrm{A}&=200 e^{-3(0.462)}=50.015=y_0 \end{aligned}$$

   Hence, $y=\mathrm{A} e^{k t}=50.015 e^{0.462 t}$

   At $t=0, y(0)=50.015 e^{0.462(0)}=50.015$, number of rabbit is integer hence it is predicted that the initial number of rabbit is $y_0=50$.

   $$y=y_0 e^{0.462 t}=2 y_0$$$$t=\frac{\ln 2}{0.462}=1.5 \text { year }$$

   b. A person has bought 1000 rabbits from the farm and releases them to the jungle that is full of predator (i.e. $p = 50$ snakes at the time he/she releases the rabbit). Given the governing equation of the rabbit population is changed to $\frac{dy}{dt}=-p+3y\left(1-\frac{y}{100}\right)$. How long does it take the rabbit population to decrease to half?

   Hint: The doubling time decrease/increase to its initial amount/quantity is related to half-life concept. Students are encouraged to study its application in engineering. For example, to compare the charging time performance of various capacitors using half-life indicator in electrical field.

   Solution

   $$\begin{aligned} & \frac{d y}{d t}=-p+3 y\left(1-\frac{y}{100}\right), t=0, y(0)=1000, p=50 \\ & \frac{d y}{d t}=-50+3 y\left(1-\frac{y}{100}\right) \qquad \rightarrow \qquad \int \frac{100}{-5000+3 y(100-y)} d y=\int d t \end{aligned}$$

   By using partial fraction decomposition:

   $$\begin{aligned} & \int \frac{-100}{3 y^2-300 y+5000} d y=\int \frac{A}{y-21.1324}+\frac{B}{3(y-78.8675)} d y \\ & \begin{array}{l} A y-21.132 A+3 B y-236.604 B=-100 \qquad \rightarrow \qquad \begin{array}{l} \text { Coefficient of } y^0: A+3 B=0 \\ \text { Coefficient of } y:-21.1324 A-236.604 B=-100 \end{array} \\ A=-1.732, B=0.5773 \end{array}>> \end{aligned}$$

   Hence,

   $$\begin{aligned} \int \frac{-1.732}{y-21.1324}+\frac{0.5773}{3(y-78.8675)} d y&=\int d t \\ -1.732 \ln |y-21.1324|+0.1924 \ln |y-78.8675|&=t+C \end{aligned}$$

   $t=0, y(0)=1000, p=50$

   $$\begin{aligned} -1.732 \ln |1000-21.1324|+0.1924 \ln |1000-78.8675|&=C\qquad\rightarrow\qquad C=-10.6140 \\ -1.732 \ln |y-21.1324|+0.1924 \ln |y-78.8675|&=t-10.6140 \end{aligned}$$

   Note: This is implicit solution for the system because the solution $y(t)$ cannot be expressed in the explicit form, i.e. $y=y(t)$.

   For the rabbit population to decrease to half, $y(t)=0.5 y_0$

   $$-1.732 \ln \vert 500-21.1324 \vert +0.1924 \ln \vert 500-78.8675 \vert=t-10.6140$$

   It takes $\mathrm{t}=1.088$ years

2. A brine mixing problem is illustrated in the following figure where a tank contains a liquid of volume $V_0=10m^3$ with concentration $C_0=0.5\frac{g}{m^3}$ initially and two valves (A & B) are opened simultaneously. The rate of change for the amount of salt in the tank over time is given: $\frac{dx}{dt}=Q_1C_1-Q_2\frac{x(t)}{V_0+(Q_1-Q_2)t}$. Let $x(t)=$ amount of salt; concentration of salt over time $=C(t)=\frac{x(t)}{V(t)}$; $Q_1=Q_2-2\frac{m^3}{\text{min}}$; $\quad C_1=1\frac{g}{m^3}$. What is the change of the amount of salt and also the change of its concentration over time.

   
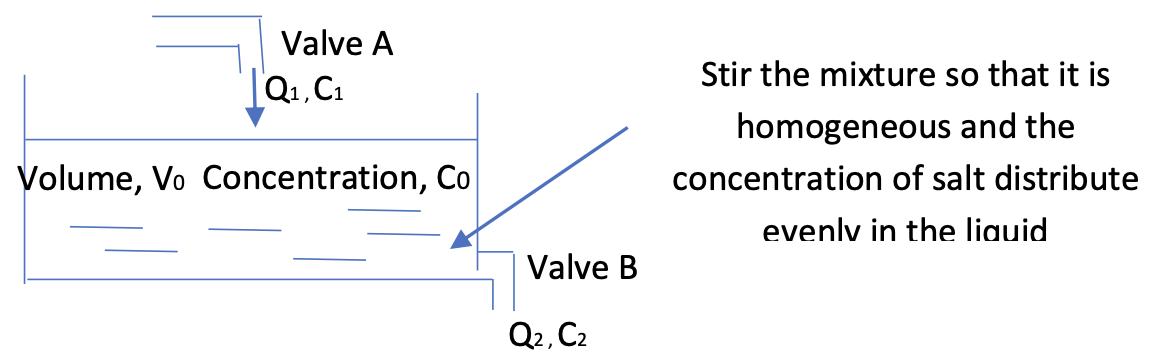   Solution

   Step 1: Linear Form

   $$\frac{d x}{d t}+\frac{2}{10+t} x=2, \quad p(t)=\frac{2}{10+t} ; \quad q(t)=2$$

   Step 2: Integrating Factor

   $$IF =e^{\int_{p(t) d t}}=e^{\int \frac{2}{10+t} d t}=e^{2 \ln (10+t)}=(10+t)^2$$

   Step 3: Multiply

   $$(10+t)^2 \frac{d x}{d t}+2(10+t) x=2(10+t)^2$$

   Step 4: Exact

   $$\frac{d}{d t}\left(x(10+t)^2\right)=2(10+t)^2$$

   Step 5: Integrate

   $$\begin{aligned} \int \frac{d}{d t}\left(x(10+t)^2\right) d t&=\int 2(10+t)^2 d t \\ x(10+t)^2&=\int 2(10+t)^2 d t \quad \\ x(10+t)^2&=\int 2\left(100+20 t+t^2\right) d t \\ x(10+t)^2&=200 t+20 t^2+\frac{2}{3} t^3+C \end{aligned}$$$$\begin{aligned} x(0)=x_0=c_0 V_0&=5 g \\ (5)(10+0)^2&=200(0)+20(0)^2+\frac{2}{3}(0)^3+C \\ 500&=C \end{aligned}$$

   $\therefore x(t)=\frac{1}{(10+t)^2}\left(200 t+20 t^2+\frac{2}{3} t^3+500\right)$ [Change of the amount of salt over time]

   $\therefore c(t)=\frac{x(t)}{V(t)}=\frac{1}{10(10+t)^2}\left(200 t+20 t^2+\frac{2}{3} t^3+500\right)$ [ Change of the concentration of salt over time]

3. The figure below shows the outflow of water from a cylindrical tank with a hole at the bottom. Determine the height of the water in the tank at any time if the tank has a diameter of 2m, the hole has diameter 1cm, and the initial height of the water when the hole is opened is 2.25m. When will the tank be empty?

   
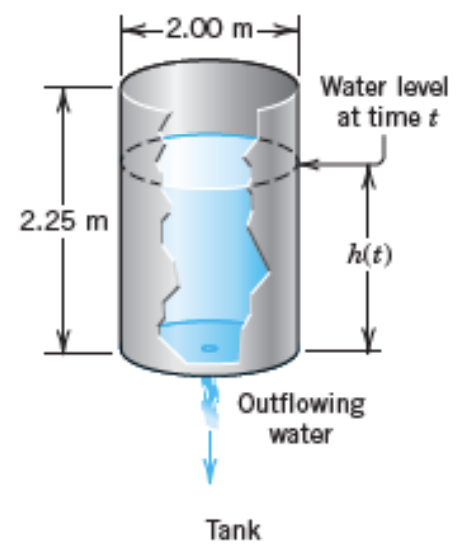   Solution

   Step 1: Setting up the model

   To get an equation, we relate the decrease in water level $h(t)$ to the outflow. The volume $\Delta V$ of the outflow during a short time $\Delta t$ is

   $$\Delta V=A v \Delta t \tag{A=\text { Area of hole }}$$

   $\Delta V$ must equal the change $\Delta V^*$ of the volume of the water in the tank. Now

   $$\Delta V^*=-B \Delta h \tag{B=\text { Cross-sectional area of tank }}$$

   where $\Delta h(>0)$ is the decrease of the height $h(t)$ of the water. The minus sign appears because the volume of the water in the tank decreases. Equating $\Delta V$ and $\Delta V^*$ gives

   $$-B \Delta h=A v \Delta t .$$

   We now express $v$ according to Torricelli's law and then let $\Delta t$ (the length of the time interval considered) approach 0 - this is a standard way of obtaining an ODE as a model. That is, we have

   $$\frac{\Delta h}{\Delta t}=-\frac{A}{B} v=-\frac{A}{B} 0.600 \sqrt{2 g h(t)}$$

   and by letting $\Delta t \rightarrow 0$ we obtain the ODE

   $$\frac{d h}{d t}=-26.56 \frac{A}{B} \sqrt{h}$$

   where $26.56=0.600 \sqrt{2 \cdot 980}$. This is our model, a first-order ODE.

   Step 2: General solution

   Our ODE is separable. $A / B$ is constant. Separation and integration gives

   $$\frac{d h}{\sqrt{h}}=-26.56 \frac{A}{B} d t \quad \text { and } \quad 2 \sqrt{h}=c^*-26.56 \frac{A}{B} t .$$

   Dividing by 2 and squaring gives $h=(c-13.28 A t / B)^2$. Inserting $13.28 A / B=13.28 \cdot 0.5^2 \pi / 100^2 \pi=0.000332$ yields the general solution

   $$h(t)=(c-0.000332 t)^2 .$$

   Step 3: Particular solution

   The initial height (the initial condition) is $h(0)=225 \mathrm{~cm}$. Substitution of $t=0$ and $h=225$ gives from the general solution $c^2=225, c=15.00$ and thus the particular solution

   $$h_p(t)=(15.00-0.000332 t)^2 .$$

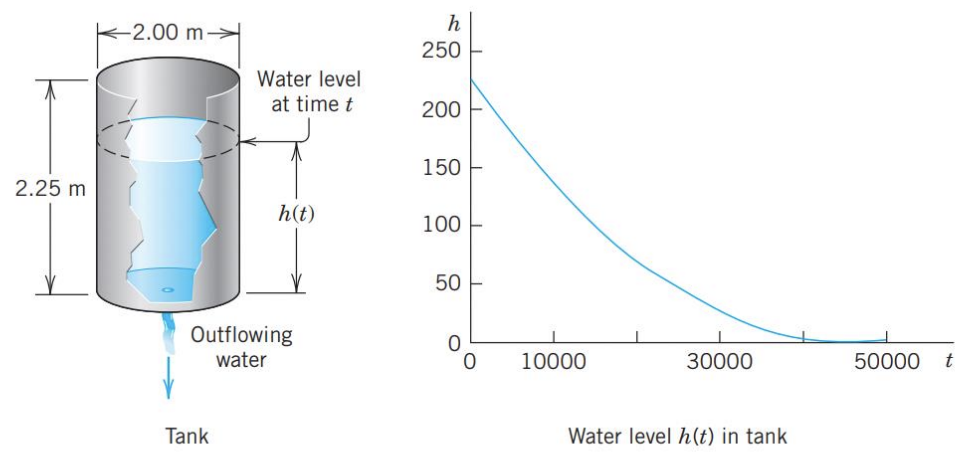
   Step 4: Tank empty

   $$h_p(t)=0 \text{ if } t=15.00 / 0.000332=45,181\text{ sec}=12.6\text{ hours}$$

   Here you see distinctly the importance of the choice of units — we have been working with the cgs system, in which time is measured in seconds! We used $g=980 \mathrm{~cm} / \mathrm{sec}^2$.

   Step 5: Checking

   Check the result.

   

4. Given the governing equation for RLC electrical circuit: $L\frac{d^2q(t)}{dt^2}+R\frac{dq(t)}{dt}+\frac{1}{C}q(t)=E(t)$. An inductor of $L = 2$ henrys and a resistor of $R = 10$ ohms are connected in series with an emf of $E$ volts. Note that in this case the capacitor has been removed. At $t = 0$, the switch $S$ is closed, thus no charge and current flow at that moment. Find the charge and current at any time $t >0$ if

   

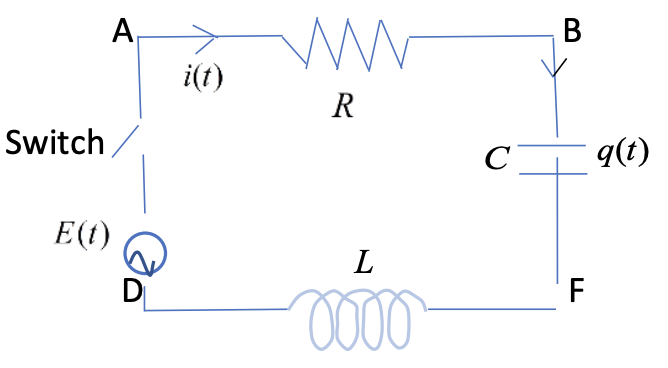
   a. $E(t) = 40$ volts

   Solution

   $$2 \frac{d i(t)}{d t}+10 i(t)=40$$

   It is linear differential equation that can is separable

   $$\begin{aligned} \int \frac{d i(t)}{20-5 i(t)}&=\int d t \frac{1}{-5} \ln \vert20-5 i\vert&=t+C \end{aligned}$$

   Apply initial condition $i(0)=0$,

   $$\begin{aligned} \frac{1}{-5} \ln |20-5(0)|&=(0)+C \\ C&=-0.599 \end{aligned}$$$$\begin{aligned} \therefore \frac{1}{-5} \ln \vert 20-5 i\vert &=t-0.599 \\ i(t)&=\frac{20-e^{-5 t+2.996}}{5}=4-\frac{1}{5} e^{-5 t+2.996}=4\left(1-e^{-5 t}\right) \tag{\text{Current}} \end{aligned}$$$$q(t)=\int 4\left(1-e^{-5 t}\right) d t=4 t+\frac{4 e^{-3 t}}{5}+C$$

   Apply initial condition $q(0)=0$,

   $$\begin{aligned} q(0)&=4(0)+\frac{4 e^{-5(0)}}{5}+C=0 \\ C&=-4 / 5 \gg \\ q(t)&=\int 4\left(1-e^{-5 t}\right) d t=4 t+\frac{4 e^{-5 t}}{5}-\frac{4}{5} \tag{Charge} \end{aligned}$$

   You can get the same answer by using linear differential equation with integrating factor:

   $$\begin{aligned} 2 \frac{d i(t)}{d t}+10 i(t)&=40 \\ \frac{d i(t)}{d t}+5 i(t)&=20 \end{aligned}$$

   where $p(t)=5 ; q(t)=5$

   $$\begin{aligned} IF&=e^{\int p(t) d t}=e^{\int 5 d t}=e^{3 t} \\ e^{3 t} \frac{d i(t)}{d t}+e^{3 t} 5 i(t)&=20 e^{3 t} \\ \frac{d}{d t}\left(e^{3 t} i\right)&=20 e^{3 t} \\ e^{5 t} i&=\int 20 e^{5 t} d t=4 e^{5 t}+C \\ i(t)&=\int 20 e^{5 t} d t=4+C e^{-5 t} \\ i(0)&=4+C e^{-5(0)}=0 C&=-4 \\ \therefore i(t)&=4\left(1-e^{-5 t}\right) \end{aligned}$$

   Hence

   $$\quad q(t)=\int 4\left(1-e^{-5 t}\right) d t=4 t+\frac{4 e^{-5 t}}{5}-\frac{4}{5}$$

   [Same answer as previous]

   Note: There are at least one method to solve the differential equation. Choose the favourable one in term of efficiency. In term of accuracy, all provide the correct answer.

   b. a. $E(t) = 20 e^{-3t}$ volts

   Solution

   $$2 \frac{d i(t)}{d t}+10 i(t)=20 e^{-3 t}$$

   It is linear differential equation that is separable

   $$\int \frac{d i(t)}{10 e^{-3 t}-5 i(t)}=\int d t$$

   Difficult to be solved in this form, try other method.

   $$\begin{aligned} 2 \frac{d i(t)}{d t}+10 i(t)&=20 e^{-3 t} \frac{d i(t)}{d t}+5 i(t)&=10 e^{-3 t} \end{aligned}$$

   where $p(t)=5 ; q(t)=10 e^{-3 t}$

   $$\begin{aligned} IF&=e^{\int p(t) d t}=e^{\int 5 d t}=e^{5 t} \\ e^{5 t} \frac{d i(t)}{d t}+e^{5 t} 5 i(t)&=10 e^{-3 t} e^{5 t} \\ \frac{d}{d t}\left(e^{5 t} i\right)&=10 e^{2 t} \\ e^{5 t} i&=\int 10 e^{2 t} d t=5 e^{2 t}+C \\ e^{5 t}(0)&=5 e^{2(0)}+C C&=-5 \end{aligned}$$

   Thus

   $$i(t)=5 e^{-3 t}-5 e^{-5 t}=5\left(e^{-3 t}-e^{-5 t}\right)$$

   Hence,

   $$\begin{aligned} q(t)&=\int 5\left(e^{-3 t}-e^{-5 t}\right) d t=\frac{5}{-3} e^{-3 t}+e^{-5 t}+C \\ q(0)&=\frac{5}{-3} e^{-3(0)}+e^{-5(0)}+C=0 \end{aligned}$$

   Hence, $C=\frac{5}{3}$

   $$\therefore q(t)=\frac{5}{-3} e^{-3 t}+e^{-5 t}+\frac{5}{3}$$

5. Let the governing equation for a vibrating car structure: $2\frac{d^2x(t)}{dt^2}+7\frac{dx(t)}{dt}+8x(t)=\underbrace{F(t)}_{\text{forcing function}}$. $x(0)=2$, $x(0)=0$. Find the total solution for the 2nd order ODE equation if the forcing function is given as follows:

   a. No excitation, $F =0$ and it is subjected to initial condition. Hence prove that the solutions are linearly independent to each other.

   Solution

   Homogeneous Part, $2\frac{d^{2} x( t)}{dt^{2}} +9\frac{dx( t)}{dt} +8x( t) =0;\quad x( 0) =2,\quad \dot{x}( 0) =0$

   Characteristic equation:

   $$\begin{aligned} 2m^{2} +7m+8 & =0\\ m & =\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)} =\frac{-7\pm \sqrt{-15}}{4} =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4} \end{aligned}$$

   Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ;\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$)

   Complementary solution:

   $$\begin{aligned} x( t) & =c_{1} e^{\left( -\frac{7}{4} +i\right) t} +c_{2} e^{\left( -\frac{7}{4} -i\right) t} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)\\ & =e^{\left( -\frac{7}{4} +i\right) t}\left( A\cos\frac{\sqrt{15}}{4} t+B\sin\frac{\sqrt{15}}{4} t\right) \end{aligned}$$

   where $e^{\pm ix} =\cos x\pm i\sin x,\ A=c_{1} +c_{2} ,\ B=i( c_{1} -c_{2})$

   Initial Value Problem

   $$\begin{gather*} x( t) =c_{1} e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) t}\\ \dot{x}( t) =\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) c_{1} e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) t} +\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) c_{1} e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) t} \end{gather*}$$$$x( 0) =c_{1} e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right)( 0)} +c_{2} e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right)( 0)} =2\Longrightarrow c_{1} +c_{2} =2 \tag{1}$$$$\begin{gather} \dot{x}( 0) =\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) c_{1} e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right)( 0)} +\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) c_{1} e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right)( 0)}\\ \Longrightarrow \left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right)( 2-c_{2}) +\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) c_{2} =0 \end{gather} \tag{2}$$

   Solving (1) and (2) simultaneously, $c_{1} =1-1.807i;\ c_{2} =1+1.807i$

   $$x( t) =( 1-1.807i) e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) t} +( 1+1.807i) e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) t}$$

   b. Repeat the same problem in 5(a) with various combinations of damping, i.e. $2\frac{d^{2} x( t)}{dt^{2}} +8\frac{dx( t)}{dt} +8x( t) =\underbrace{F(t)}_{\text{forcing function}}$.

   Solution

   Homogeneous Part, $2\frac{d^{2} x( t)}{dt^{2}} +9\frac{dx( t)}{dt} +8x( t) =0;\quad x( 0) =2,\quad \dot{x}( 0) =0$

   Characteristic equation:

   $$\begin{aligned} 2m^{2} +8m+8 & =0\\ m & =\frac{-8\pm \sqrt{8^{2} -4( 2)( 8)}}{2( 2)} =\frac{-8\pm \sqrt{0}}{4} =-\frac{8}{4} =-2 \end{aligned}$$

   Comment: Repeated real root ($m_{1} =m_{2} =-2$)

   Complementary solution: $x( t) =c_{1} e^{-2t} +c_{2} te^{-2t}$

   Initial Value Problem

   $$\begin{gather*} x( t) =c_{1} e^{-2t} +c_{2} te^{-2t}\\ \dot{x}( t) =-2c_{1} e^{-2t} +c_{2} t( -2) e^{-2t} +e^{-2t} c_{2} \end{gather*}$$$$\begin{aligned} x( 0) & =c_{1} e^{( -2)( 0)} +c_{2}( 0) e^{( -2)( 0)} =2\Longrightarrow c_{1} =2 \end{aligned}$$$$\dot{x}( 0) =-2( 2) e^{( -2)( 0)} +c_{2}( 0)( -2) e^{( -2)( 0)} +e^{( -2)( 0)} c_{2} =0\Longrightarrow c_{2} =4$$$$\mathbf{x( t) =2e^{-2t} +4te^{-2t}}$$

   c. Repeat the same problem in 5(a) with various combinations of damping, i.e. $2\frac{d^{2} x( t)}{dt^{2}} +9\frac{dx( t)}{dt} +8x( t) =\underbrace{F(t)}_{\text{forcing function}}$.

   Solution

   Homogeneous Part, $2\frac{d^{2} x( t)}{dt^{2}} +9\frac{dx( t)}{dt} +8x( t) =0;\quad x( 0) =2,\quad \dot{x}( 0) =0$

   Characteristic equation:

   $$\begin{aligned} 2m^{2} +9m+8 & =0\\ m & =\frac{-9\pm \sqrt{9^{2} -4( 2)( 8)}}{2( 2)} =\frac{-9\pm \sqrt{17}}{4} \end{aligned}$$

   Comment: Real and distinct root ($m_{1} =-1.2192;\ m_{2} =-3.2808$)

   Complementary solution: $x( t) =c_{1} e^{( -1.2192) t} +c_{2} e^{( -3.2808) t}$

   Initial Value Problem

   $$\begin{gather*} x( t) =c_{1} e^{( -1.2192) t} +c_{2} e^{( -3.2808) t}\\ \dot{x}( t) =-1.2192c_{1} e^{( -1.2192) t} -3.2808c_{2} e^{( -3.2808) t} \end{gather*}$$$$\begin{aligned} x( 0) & =c_{1} e^{( -1.2192)( 0)} +c_{2} e^{( -3.2808)( 0)} =2\Longrightarrow c_{1} +c_{2} =2 \end{aligned}$$$$\dot{x}( 0) =-1.2192c_{1} e^{( -1.2192)( 0)} -3.2808c_{2} e^{( -3.2808)( 0)} =0\Longrightarrow -1.2192c_{1} -3.2808c_{2} e=0$$

   Solving (1) and (2) simultaneously, $c_{1} =3.1828;\ c_{2} =-1.1828$

   $$\mathbf{x( t) =3.1828e^{( -1.2192) t} -1.1828e^{( -3.2808) t}}$$

6. Continue the problem 5. Let the governing equation for a vibrating car structure: $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =\underbrace{F(t)}_{\text{forcing function}}$, $x( 0) =2,\ \dot{x}( 0) =0$. Find the total solution for the 2nd order ODE equation if the forcing function is given as follows:

   a. Engine excitation $F( t) =5\cos 10t$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5\cos 10t$, $r( t) =e^{\alpha t} P_{n}( t) =5\cos 10t=5Re\left[ e^{i10t}\right]$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For exponential function, $5Re\left[ e^{i10t}\right]$, $\alpha =10i,\ n=0$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, Assume $x_{p,real} =Re[ x_{p}]$, $x_{p}( t) =e^{( \alpha t)} Q_{n}( t) =Ae^{( 10it)}$ Differentiate it gives,$\begin{aligned}\frac{d}{dx}( x_{p}( t)) & =10iAe^{( 10it)}\\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =-100Ae^{( 10it)}\end{aligned}$ Then, we get $\begin{aligned}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =5\cos 10t\\2\left( -100Ae^{( 10it)}\right) +7\left( 10iAe^{( 10it)}\right) +8\left( Ae^{( 10it)}\right) & =5\cos 10t\\e^{( 10it)}( -192A+70iA) & =5e^{( 10it)}\end{aligned}$ Comparing the coefficient, $( -192A+70iA) =5\Longrightarrow A=\frac{5}{70i-192}$ Actual particular solution, $\begin{aligned}x_{p}( t) & =\frac{5}{70i-192} e^{( 10it)}\\& =\frac{5}{70i-192}(\cos 10t+i\sin 10t)\frac{-70i-192}{-70i-192}\\& =\frac{( -960\cos 10t+350\sin 10t) +i( -350\cos 10t-960\sin 10t)}{41764}\end{aligned}$ $x_{p,real}( t) =Re[ x_{p}] =-0.02299\cos 10t+0.00838\sin 10t$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5\cos 10t$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -0.02299\cos 10t+0.00838\sin 10t$.

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -0.02299\cos 10( 0) +0.00838\sin 10( 0) =2\Longrightarrow c_{1} +c_{2} =2.02299$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)\\ & -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +0.2299\sin 10t+0.0838\cos 10t\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right)\\ & -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +0.2299\sin 10( 0) +0.0838\cos 10( 0)\\ \dot{x}( 0) & \left( 2.02299i\frac{\sqrt{15}}{4} -c_{2} i\frac{2\sqrt{15}}{4}\right) -\frac{7}{4}( 2.02299) +0.838=0 \end{aligned}$$

   $c_{2} =\frac{3.4564-1.9588i}{-1.9365i} \times \frac{i}{i} =1.7849i+1.0115;\quad c_{1} =1.0115-1.7849i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 1.0115-1.7849i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 1.0115-1.7849i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) -0.02299\cos 10t+0.00838\sin 10t}$

   b. Engine excitation $F( t) =8\sin 8t$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =8\sin 8t$, $r( t) =e^{\alpha t} P_{n}( t) =8\sin 8t=8Im\left[ e^{i8t}\right]$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For exponential function, $8Im\left[ e^{i8t}\right]$, $\alpha =8i,\ n=0$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, Assume $x_{p,real} =Im[ x_{p}]$, $x_{p}( t) =e^{( \alpha t)} Q_{n}( t) =Ae^{( 8it)}$ Differentiate it gives, $\begin{aligned}\frac{d}{dx}( x_{p}( t)) & =8iAe^{( 8it)}\\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =-64Ae^{( 8it)}\end{aligned}$ Then, we get $\begin{aligned}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =8\sin 8t\\2\left( -64Ae^{( 8it)}\right) +7\left( 8iAe^{( 8it)}\right) +8\left( Ae^{( 8it)}\right) & =8\sin 8t\\e^{( 8it)}( 56i-120) A & =8e^{( 8it)}\end{aligned}$ Comparing the coefficient, $( 56i-120) A=8\Longrightarrow A=\frac{8}{56i-120}$ Actual particular solution, $\begin{aligned}x_{p}( t) & =\frac{8}{56i-120} e^{( 8it)}\\& =\frac{8}{56i-120}(\cos 8t+i\sin 8t)\frac{-56i-120}{-56i-120}\\& =\frac{( 448\sin 8t-960\cos 8t) +i( -448\cos 8t-960\sin 8t)}{17536}\end{aligned}$ $x_{p,real}( t) =Im[ x_{p}] =-\frac{7}{274}\cos 8t-\frac{15}{274}\sin 8t$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =8\sin 8t$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{274}\cos 8t-\frac{15}{274}\sin 8t$

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{274}\cos 8( 0) -\frac{15}{274}\sin 8( 0) =2\Longrightarrow c_{1} +c_{2} =2.0255$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)\\ & -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{56}{274}\cos 8t-\frac{90}{274}\sin 8t\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right)\\ & -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +\frac{56}{274}\cos 8( 0) -\frac{90}{274}\sin 8( 0) =0 \end{aligned}$$

   $c_{2} =\frac{3.9826-1.9612i}{-1.9364i} \times \frac{i}{i} =2.0567i+1.0128;\quad c_{1} =1.028-2.0567i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 1.0128-2.0567i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 1.0128+2.0567i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{274}\cos 8t-\frac{15}{274}\sin 8t}$

   c. Engine excitation $F( t) =e^{-10t}$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =e^{-10t}$, $r( t) =e^{\alpha t} P_{n}( t) =e^{-10t}$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For exponential function, $\alpha =-10,\ n=0$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, $x_{p}( t) =e^{( \alpha t)} Q_{n}( t) =Ae^{( -10t)}$ Differentiate it gives, $\begin{aligned}\frac{d}{dx}( x_{p}( t)) & =-10Ae^{( -10t)}\\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =100Ae^{( -10t)}\end{aligned}$ Then, we get $\begin{aligned}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =e^{( -10t)}\\2\left( 100Ae^{( -10t)}\right) +7\left( -10Ae^{( -10t)}\right) +8\left( Ae^{( -10t)}\right) & =e^{( -10t)}\\e^{( 8it)}( 200-70+8) A & =e^{( -10t)}\end{aligned}$ Comparing the coefficient, $138A=1\Longrightarrow A=\frac{1}{138}$ Actual particular solution, $x_{p}( t) =e^{( \alpha t)} Q_{n}( t) =\frac{1}{138} e^{( -10t)}$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =e^{-10t}$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +\frac{1}{138} e^{-10t}$

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +\frac{1}{138} e^{-10( 0)} =2\Longrightarrow c_{1} +c_{2} =1.9928$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{10}{138} e^{-10t}\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{10}{138} e^{-10( 0)} =0 \end{aligned}$$

   $c_{2} =\frac{3.5599-1.9295i}{-1.9365i} \times \frac{i}{i} =1.8383i+0.9964;\quad c_{1} =0.9964-1.8383i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 0.9964-1.8383i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 0.9964+1.8383i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) +\frac{1}{138} e^{-10t}}$

   d. Engine excitation $F( t) =5e^{-10t}\cos 10t$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $\begin{array}{l}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5e^{-10t}\cos 10t,\\\begin{aligned} r( t) & =e^{\alpha t} P_{n}( t) =5e^{-10t}\cos 10t\\ & =5e^{-10t} Re\left[ e^{i10t}\right] =Re\left[ 5e^{( -10+10i) t}\right] \end{aligned} \end{array}$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For exponential function, $Re\left[ 5e^{( -10+10i) t}\right]$, $\alpha =-10+10i,\ n=0$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, $\begin{aligned} x_{p}( t) & =e^{( \alpha t)} Q_{n}( t) =Ae^{( -10t)} \end{aligned}$ Assume $x_{p,real} =Re[ x_{p}]$, $\begin{aligned} x_{p}( t) & =e^{( \alpha t)} Q_{n}( t) =Ae^{( -10+10i) t} \end{aligned}$ Differentiate it gives, $\begin{aligned} \frac{d}{dx}( x_{p}( t)) & =( -10+10i) Ae^{( -10+10i) t}\\& \\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =( -200i) Ae^{( -10+10i) t}\end{aligned}$ Then, we get $\begin{aligned} 2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =5e^{-10t}\cos 10t\\ 2\left(( -200i) Ae^{( -10+10i) t}\right) +7\left(( -10+10i) Ae^{( -10+10i) t}\right) +8\left( Ae^{( -10+10i) t}\right) & =5e^{( -10+10i) t}\\ e^{( -10+10i) t}( 2( -200i) +7( -10+10i) +8) A & =5e^{( -10+10i) t} \end{aligned}$ Comparing the coefficient, $( 2( -200i) +7( -10+10i) +8) A=5\Longrightarrow A=\frac{5}{-62-330i}$ Actual particular solution, $\begin{aligned} x_{p}( t) & =e^{( \alpha t)} Q_{n}( t) =\frac{5}{-62-330i} e^{( -10+10i) t}\\& =\frac{5}{-62-330i} e^{( -10) t}(\cos 10t+i\sin 10t) \times \frac{-63+330i}{-63+330i}\\& =\frac{( -1650\sin 10t-310\cos 10t) +i( 1650\cos 10t-310\sin 10t)}{112744} e^{( -10) t} \end{aligned}$ $x_{p,real}( t) =Re[ x_{p}] =( -0.01463\sin 10t-0.002750\cos 10t) e^{( -10) t}$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5e^{-10t}\cos 10t$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +( -0.01463\sin 10t-0.002750\cos 10t) e^{( -10) t}$

   Initial Value Problem

   $$\begin{aligned} x( 0) &=e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +( -0.01463\sin 10( 0) -0.002750\cos 10( 0)) e^{(-10)(0)} =2\\ c_{1} +c_{2} &=2.0028 \end{aligned}$$$$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)\\ & +( -0.1463\cos 10t+0.0275\sin 10t) e^{( -10) t} +( 0.1463\sin 10t+0.0275\cos 10t) e^{( -10) t}\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right)\\ & +( -0.1463\cos 10( 0) +0.0275\sin 10( 0)) e^{( -10) 0} +( 0.1463\sin 10( 0) +0.0275\cos 10( 0)) e^{( -10) 0} =0 \end{aligned}$$

   $c_{2} =\frac{3.6237-1.9392i}{-1.9365} \times \frac{i}{i} =1.8713+1.0014i;\quad c_{1} =3.8741-1.0014i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 3.8741-1.0014i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 1.8713+1.0014i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) +( -0.01463\sin 10t-0.002750\cos 10t) e^{( -10) t}}$

   e. Road excitation $F( t) =10$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $\begin{array}{l}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =10,\\r( t) =e^{\alpha t} P_{n}( t) =10\end{array}$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For polynomial function, $10$, $\alpha =0,\ n=0$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, $x_{p} =e^{( \alpha t)} Q_{n}( t) =A$ Differentiate it gives, $\begin{aligned}\frac{d}{dx}( x_{p}( t)) & =0\\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =0\end{aligned}$ Then, we get $\begin{aligned}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =10\\2( 0) +7( 0) +8A & =10\\A & =1.25\end{aligned}$ Actual particular solution,$x_{p}( t) =1.25$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =10$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +1.25$

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +1.25=2\Longrightarrow c_{1} +c_{2} =0.75$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) =0\\ \dot{x}( 0) & =\left( i\frac{\sqrt{15}}{4} c_{1} -i\frac{\sqrt{15}}{4} c_{2}\right) -\frac{7}{4}( c_{1} +c_{2}) =0 \end{aligned}$$

   $i\frac{\sqrt{15}}{4}( 0.75-c_{2}) -i\frac{\sqrt{15}}{4} c_{2} -\frac{7}{4}( 0.75) =0\Longrightarrow c_{2} =0.3750+0.6778i;\ c_{1} =0.3750-0.6778i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 0.3750-0.6778i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 0.3750+0.6778i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) +1.25}$

   f. Road excitation $F( t) =5t^{2} +7t+9$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5t^{2} +7t+9,$ $r( t) =e^{\alpha t} P_{n}( t) =5t^{2} +7t+9$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   For polynomial function, $5t^{2} +7t+9$, $\alpha =0,\ n=2$ Since $\alpha \neq m_{1} \ \text{or} \ m_{2}$, $x_{p} =e^{( \alpha t)} Q_{n}( t) =At^{2} +Bt+C$ Differentiate it gives, $\begin{aligned}\frac{d}{dx}( x_{p}( t)) & =2At+B\\\frac{d^{2}}{dx^{2}}( x_{p}( t)) & =2A\end{aligned}$ Then, we get $\begin{aligned}2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) & =5t^{2} +7t+9\\2( 2A) +7( 2At+B) +8\left( At^{2} +Bt+C\right) & =5t^{2} +7t+9\\4A+7B+8C+14At+8Bt+8A^{2} t & =5t^{2} +7t+9\end{aligned}$ Comparing coefficients, $t^{2} :\quad 8A=5\Longrightarrow A=0.625$ $t:\quad 14A+8B=7\Longrightarrow 14( 0.625) +8B=7\Longrightarrow B=-0.2188$ $t^{0} :\quad 4A+7B+8C=9\Longrightarrow 4( 0.625) +8) -0.2188) +8C=9\Longrightarrow C=1.0040$ Actual particular solution, $x_{p}( t) =0.625t^{2} -0.2188B+1.0040$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =5t^{2} +7t+9$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +0.625t^{2} -0.2188t+1.0040$

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +0.625( 0)^{2} -0.2188( 0) +1.0040=2\Longrightarrow c_{1} +c_{2} =0.996$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +1.25t-0.2188\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +1.25( 0) -0.2188=0\\ \dot{x}( 0) & =\left( i\frac{\sqrt{15}}{4} c_{1} -i\frac{\sqrt{15}}{4} c_{2}\right) -\frac{7}{4}( c_{1} +c_{2}) -0.2188=0 \end{aligned}$$

   $\Longrightarrow c_{2} =\frac{1.9618-0.9644i}{-1.9365i} =0.4980+1.0131i;\ c_{1} =0.4980-1.0131i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 0.4980-1.0131i) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 0.4980+1.0131i) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) +0.625t^{2} -0.2188t+1.0040}$

   g. Road excitation $F( t) =6te^{t} +3t$

   Solution

   Step 1: Homogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =0$

   Step 2: Nonhomogeneous Part $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =6te^{t} +3t,$ $r( t) =e^{\alpha t} P_{n}( t) =6te^{t} +3t$

   Characteristic equation: $\begin{aligned}2m^{2} +7m+8 & =0\\m & =-\frac{-7\pm \sqrt{7^{2} -4( 2)( 8)}}{2( 2)}\\& =\frac{-7\pm \sqrt{-15}}{4}\\& =-\frac{7}{4} \pm i\frac{\sqrt{15}}{4}\end{aligned}$ Comment: A pair of complex conjugates roots ($m_{1} =-\frac{7}{4} +i\frac{\sqrt{15}}{4} ,\ m_{2} =-\frac{7}{4} -i\frac{\sqrt{15}}{4}$) Complementary solution: $x( t) = e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right)$

   $\begin{aligned}u_{i}( t) & =-\int \frac{r( t) x_{2}( t)}{W( y_{1} ,y_{2})} dt=-\int \frac{\left( 6te^{t} +3t\right) e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) t}}{-i\frac{2\sqrt{15}}{4} e^{-\frac{14}{4} t}} dt\\& =-\frac{12}{\sqrt{15}} i\int te^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t} dt-\frac{6}{\sqrt{15}} i\int te^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t} dt\end{aligned}$ Integration by part, $\begin{aligned}&-\frac{12}{\sqrt{15}} i\int \underbrace{t}_{u}\underbrace{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t} dt}_{dv}\\&=-\frac{12}{\sqrt{15}} i\left[\underbrace{t}_{u}\underbrace{\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)}}_{v} -\int \underbrace{\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)}}_{v}\underbrace{dt}_{du}\right]\\&=-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}&-\frac{6}{\sqrt{15}} i\int te^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t} dt\\&=-\frac{6}{\sqrt{15}} i\left[\underbrace{t}_{u}\underbrace{\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)}}_{v} -\int \underbrace{\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)}}_{v}\underbrace{dt}_{du}\right]\\&=-\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}u_{1}( t) &=-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\&-\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}u_{2}( t) & =\int \frac{r( t) x_{1}( t)}{W( x_{1} ,x_{2})} dt=\int \frac{\left( 6te^{t} +3t\right) e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) t}}{-i\frac{2\sqrt{15}}{4} e^{-\frac{14}{4} t}} dt\\& =\frac{12}{\sqrt{15}} i\int te^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t} +\frac{6}{\sqrt{15}} i\int te^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t} dt\end{aligned}$ Integration by part, $\begin{aligned}&\frac{12}{\sqrt{15}} i\int \underbrace{t}_{u}\underbrace{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t} dt}_{dv}\\&=\frac{12}{\sqrt{15}} i\left[\underbrace{t}_{u}\underbrace{\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)}}_{v} -\int \underbrace{\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)}}_{v}\underbrace{dt}_{du}\right]\\&=\frac{12}{\sqrt{15}} i\left[ t\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}&\frac{6}{\sqrt{15}} i\int te^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t} dt\\&=\frac{6}{\sqrt{15}} i\left[\underbrace{t}_{u}\underbrace{\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)}}_{v} -\int \underbrace{\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}}_{v}\underbrace{dt}_{du}\right]\\&=\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}&\frac{6}{\sqrt{15}} i\int te^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t} dt\\&=\frac{6}{\sqrt{15}} i\left[\underbrace{t}_{u}\underbrace{\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)}}_{v} -\int \underbrace{\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}}_{v}\underbrace{dt}_{du}\right]\\&=\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}u_{2}( t) &=\frac{12}{\sqrt{15}} i[ t\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)^{2}}\\ &+\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $x_{p} =u_{1}( t) x_{1}( t) +u_{2}( t) x_{2}( t)$ where: $\begin{aligned}u_{1}( t) x_{1}( t) & =\{-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& -\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75-i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\} e^{\left( -\frac{7}{4} +i\frac{\sqrt{15}}{4}\right) t}\\& =-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& -\frac{6}{\sqrt{15}} i\left[ t\frac{1}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)} -\frac{1}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned} u_{1}( t) x_{1}( t) & =\{\frac{12}{\sqrt{15}} i[ t\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 2.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)^{2}}\\& +\frac{6}{\sqrt{15}} i\left[ t\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{\left( 1.75+i\frac{\sqrt{15}}{4}\right) t}}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\} e^{\left( -\frac{7}{4} -i\frac{\sqrt{15}}{4}\right) t}\\& =\frac{12}{\sqrt{15}} i[ t\frac{e^{t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)^{2}}\\& +\frac{6}{\sqrt{15}} i\left[ t\frac{1}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{1}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\end{aligned}$ $\begin{aligned}x_{p}( t) & =u_{1}( t) x_{1}( t) +u_{2}( t) x_{2}( t)\\& =-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)} -\frac{e^{t}}{\left( 2.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& +\frac{12}{\sqrt{15}} i\left[ t\frac{e^{t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)} -\frac{e^{t}}{\left( 2.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& -\frac{6}{\sqrt{15}} i\left[ t\frac{1}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)} -\frac{1}{\left( 1.75-i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& +\frac{6}{\sqrt{15}} i\left[ t\frac{1}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)} -\frac{1}{\left( 1.75+i\frac{\sqrt{15}}{4}\right)^{2}}\right]\\& =-\frac{12}{\sqrt{15}} i\left[ t\frac{e^{t}\left( 2.75-i\frac{\sqrt{15}}{4}\right)}{8.5} -\frac{e^{t}\left( 6.625+i1.375\sqrt{15}\right)}{72.25}\right]\\& +\frac{12}{\sqrt{15}} i\left[ t\frac{e^{t}\left( 2.75-i\frac{\sqrt{15}}{4}\right)}{8.5} -\frac{e^{t}\left( 6.625-i1.375\sqrt{15}\right)}{72.25}\right]\\& -\frac{6}{\sqrt{15}} i\left[ t\frac{\left( 1.75+i\frac{\sqrt{15}}{4}\right)}{4} -\frac{\left( 2.125+i0.875\sqrt{15}\right)}{16}\right]\\& +\frac{6}{\sqrt{15}} i\left[ t\frac{\left( 1.75-i\frac{\sqrt{15}}{4}\right)}{4} -\frac{\left( 2.125-i0.875\sqrt{15}\right)}{16}\right]\\& =\left[ -\frac{24}{\sqrt{15}} it\frac{e^{t}\left( i\frac{\sqrt{15}}{4}\right)}{8.5} +\frac{24}{\sqrt{15}} i\frac{e^{t}\left( i1.375\sqrt{15}\right)}{8.5}\right]\\& +\left[ -\frac{12}{\sqrt{15}} it\frac{\left( i\frac{\sqrt{15}}{4}\right)}{4} +\frac{12}{\sqrt{15}} i\frac{\left( i0.875\sqrt{15}\right)}{16}\right]\\& =\left[ +\frac{12}{17} te^{t} -\frac{132}{289} e^{t} +\frac{3}{4} e^{t} -\frac{21}{32}\right]\end{aligned}$

   The complete/general solution to $2\frac{d^{2} x( t)}{dt^{2}} +7\frac{dx( t)}{dt} +8x( t) =6te^{t} +3t$ is $x_{total} =x_{c} +x_{p} =e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +\frac{12}{17} te^{t} -\frac{132}{289} e^{t} +\frac{3}{4} e^{t} -\frac{21}{32}$

   Initial Value Problem

   $x( 0) =e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +\frac{12}{17}( 0) e^{0} -\frac{132}{289} e^{0} +\frac{3}{4} e^{0} -\frac{21}{32} =2\Longrightarrow c_{1} +c_{2} =2.363$

   $$\begin{aligned} \dot{x}_{total} & =e^{\left( -\frac{7}{4}\right) t}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) t}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) t} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) t}\right) +\frac{12}{17}\left( e^{t}( 1+t)\right) -\frac{132}{289} e^{t} +\frac{3}{4} e^{t}\\ \dot{x}( 0) & =e^{\left( -\frac{7}{4}\right) 0}\left( i\frac{\sqrt{15}}{4} c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} -i\frac{\sqrt{15}}{4} c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) -\frac{7}{4} e^{\left( -\frac{7}{4}\right) 0}\left( c_{1} e^{\left( i\frac{\sqrt{15}}{4}\right) 0} +c_{2} e^{\left( -i\frac{\sqrt{15}}{4}\right) 0}\right) +\frac{12}{17}\left( e^{0}( 1+0)\right) -\frac{132}{289} e^{0} +\frac{3}{4} e^{0} =0\\ \dot{x}( 0) & =\left( i\frac{\sqrt{15}}{4} c_{1} -i\frac{\sqrt{15}}{4} c_{2}\right) -\frac{7}{4}( c_{1} +c_{2}) +0.9991=0 \end{aligned}$$

   $\Longrightarrow \ c_{1} =1.1815-1.6195i,\ c_{2} =1.1815+1.6195i$

   $\mathbf{x( t) =e^{\left( -\frac{7}{4}\right) t}\left(( 1.1815-1.6195) e^{\left( i\frac{\sqrt{15}}{4}\right) t} +( 1.1815+1.6195) e^{\left( i\frac{\sqrt{15}}{4}\right) t}\right) +}\frac{12}{17} te^{t} -\frac{132}{289} e^{t} +\frac{3}{4} e^{t} -\frac{21}{32}$